题目内容
【题目】一种药在病人血液中的含量不低于2克时,它才能起到有效治疗的作用,已知每服用![]() 且
且![]() 克的药剂,药剂在血液中的含量
克的药剂,药剂在血液中的含量![]() 克
克![]() 随着时间
随着时间![]() 小时
小时![]() 变化的函数关系式近似为
变化的函数关系式近似为![]() ,其中
,其中 .
.
![]() 若病人一次服用9克的药剂,则有效治疗时间可达多少小时?
若病人一次服用9克的药剂,则有效治疗时间可达多少小时?
![]() 若病人第一次服用6克的药剂,6个小时后再服用3m克的药剂,要使接下来的2小时中能够持续有效治疗,试求m的最小值.
若病人第一次服用6克的药剂,6个小时后再服用3m克的药剂,要使接下来的2小时中能够持续有效治疗,试求m的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
![]() 由
由![]() 可得函数y的解析式,可令
可得函数y的解析式,可令![]() ,分段解不等式求并集即可;
,分段解不等式求并集即可;
![]() 由当
由当![]() ,可得函数y的解析式,化简,结合函数的单调性,可得最小值.
,可得函数y的解析式,化简,结合函数的单调性,可得最小值.
(1)由题意,当![]() 可得
可得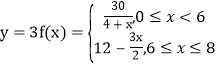 ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
综上可得![]() ,
,
所以病人一次服用9克的药剂,则有效治疗时间可达![]() 小时;
小时;
![]() 当
当![]() 时,
时,![]() ,
,
由![]() ,
,![]() 在
在![]() 均为减函数,
均为减函数,
可得![]() 在
在![]() 递减,即有
递减,即有![]() ,
,
由![]() ,可得
,可得![]() ,可得m的最小值为
,可得m的最小值为![]() .
.

练习册系列答案
相关题目
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.