题目内容
9.已知曲线C的极坐标方程是ρ=2sinθ,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=2+3t}\end{array}\right.$(t为参数).(1)写出直线l与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换$\left\{\begin{array}{l}{x′=2x}\\{y′=y}\end{array}\right.$得到曲线C′,再将曲线C′的图象向下平移一个单位,得到曲线C0.设曲线C0上任意一点M(x,y),求x+2$\sqrt{3}$y的最大值.
分析 (1)直接消去参数t得直线l的普通方程,根据ρ2=x2+y2可得曲线C的直角坐标方程;
(2)先根据伸缩变换得到曲线C′的方程,然后将曲线C′的图象向下平移一个单位,得到曲线C0,设M的坐标代入x+2$\sqrt{3}$y,根据三角函数的性质可求出所求.
解答 解:(1)曲线C的极坐标方程是ρ=2sinθ,直角坐标方程为x2+y2=2y,
直线l的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=2+3t}\end{array}\right.$,普通方程为3x-y-1=0;
(2)伸缩变换$\left\{\begin{array}{l}{x′=2x}\\{y′=y}\end{array}\right.$,即$\left\{\begin{array}{l}{x=\frac{1}{2}x′}\\{y=y′}\end{array}\right.$,代入x2+y2=2y可得$\frac{x{′}^{2}}{4}$+(y′-1)2=1,
将曲线C′的图象向下平移一个单位,得到曲线C0:$\frac{x{′}^{2}}{4}$+(y′-2)2=1,
设x′=2cosα,y′=2+sinα,
∴x+2$\sqrt{3}$y=2cosα+2$\sqrt{3}$(2+sinα)=4$\sqrt{3}$+2$\sqrt{13}$sin(α+θ),
∴x+2$\sqrt{3}$y的最大值是4$\sqrt{3}$+2$\sqrt{13}$.
点评 本题主要考查了极坐标方程,参数方程化直角坐标方程,以及椭圆的参数方程在求最值上的应用和三角函数求出最值,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
18.方程-sinx=($\frac{1}{2}$)x在区间(0,100π)内解的个数是( )
| A. | 98 | B. | 100 | C. | 102 | D. | 200 |
18.下列各项表示同一个函数的是( )
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1 | B. | f(x)=$\sqrt{{x}^{2}}$-1与g(x)=x-1 | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=$\sqrt{-2{x}^{3}}$与g(x)=x$\sqrt{-2x}$ |
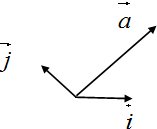 如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$
如图,在同一平面内,向量$\overrightarrow a$与单位向量$\overrightarrow i、\overrightarrow j$的夹角分别为30°、90°,已知$|\overrightarrow a|$=$2\sqrt{3}$