题目内容
设椭圆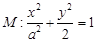
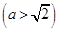 的右焦点为
的右焦点为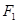 ,直线
,直线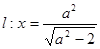 与
与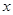 轴交于点
轴交于点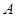 ,若
,若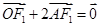 (其中
(其中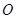 为坐标原点).
为坐标原点).
(Ⅰ)求椭圆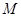
 的方程;
的方程;
(Ⅱ)设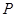 是椭圆
是椭圆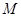 上的任意一点,
上的任意一点,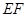 为圆
为圆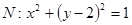 的任意一条直径(
的任意一条直径(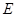 ,
,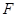 为直径的两个端点),求
为直径的两个端点),求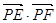 的最大值.
的最大值.
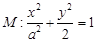
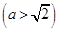 的右焦点为
的右焦点为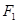 ,直线
,直线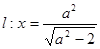 与
与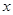 轴交于点
轴交于点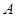 ,若
,若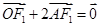 (其中
(其中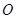 为坐标原点).
为坐标原点).(Ⅰ)求椭圆
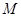
 的方程;
的方程;(Ⅱ)设
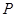 是椭圆
是椭圆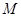 上的任意一点,
上的任意一点,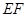 为圆
为圆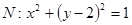 的任意一条直径(
的任意一条直径(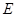 ,
,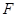 为直径的两个端点),求
为直径的两个端点),求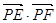 的最大值.
的最大值.解:(I)由题设知,
 ,
, ,………………………………2分
,………………………………2分由
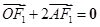 ,得
,得 .…………………………………4分
.…………………………………4分解得
 .所以椭圆
.所以椭圆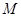 的方程为
的方程为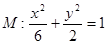 .………………………………………6分
.………………………………………6分(Ⅱ)解法1:设圆
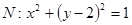 的圆心为
的圆心为 ,
,则
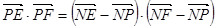
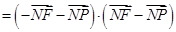

 .……………………………………………………………9分
.……………………………………………………………9分设
 是椭圆
是椭圆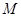 上一点,则
上一点,则 ,
,所以
 . ……………………………………………12分
. ……………………………………………12分因为
 ,所以当
,所以当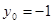 时,
时,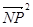 取得最大值12.
取得最大值12. 所以
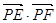 的最大值为11.……………………………………………………………………15分
的最大值为11.……………………………………………………………………15分解法2:设点
 ,所以
,所以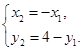 ,可得
,可得


 .…
.…因为点
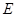 在圆
在圆 上,所以
上,所以 ,即
,即 .
. 又因为点
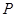 在椭圆
在椭圆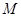 上,所以
上,所以 ,即
,即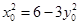 .
.所以

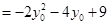
 .
. 因为
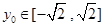 ,所以当
,所以当 时,
时,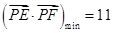 .
.略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
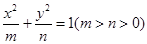 与曲线
与曲线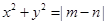 有公共点,则椭圆的离心率
有公共点,则椭圆的离心率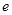 的取值范围是_________________.
的取值范围是_________________.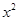 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.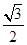 的椭圆
的椭圆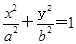 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.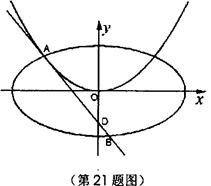
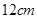 的圆柱被与底面成
的圆柱被与底面成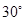 的平面所截,其截口是一个椭圆,则这个椭圆的离心率为 .
的平面所截,其截口是一个椭圆,则这个椭圆的离心率为 .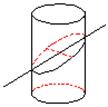
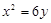 的焦点为F,椭圆C:
的焦点为F,椭圆C: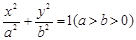 的离心率为
的离心率为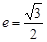 ,
,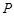 是它们的一个交点,且
是它们的一个交点,且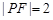 .
.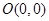 ,点A,B为椭圆
,点A,B为椭圆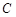 上的两点,且弦AB不平行于对称轴,
上的两点,且弦AB不平行于对称轴,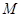 是
是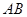 的中点,试探究
的中点,试探究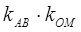 是否为定值,若不是,请说明理由。
是否为定值,若不是,请说明理由。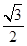 的椭圆
的椭圆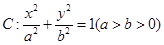 过点M(2,1),O为坐标原点,平行于OM的直线
过点M(2,1),O为坐标原点,平行于OM的直线 交椭圆C于不同的两点A、B。
交椭圆C于不同的两点A、B。 面积的最大值;
面积的最大值;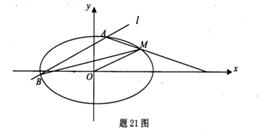
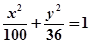 上一点P到它的右准线的距离为10, 则点P到它的左焦点的距离是( )
上一点P到它的右准线的距离为10, 则点P到它的左焦点的距离是( )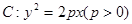 的准线为
的准线为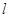 ,焦点为F,
,焦点为F,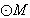 的圆心在
的圆心在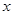 轴的正半轴上,且与
轴的正半轴上,且与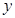 轴相切,过原点O作倾斜角为
轴相切,过原点O作倾斜角为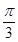 的直线
的直线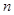 ,交
,交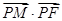 的最小值;
的最小值;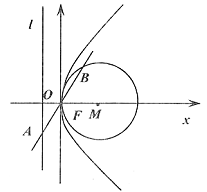
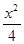 +y2=1.过点(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
+y2=1.过点(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.