题目内容

18．函数$f（x）={e^{1-{x^2}}}$（e=2.71828…为自然对数的底数）的部分图象大致是（　　）
A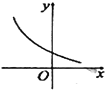．B．C．D．

分析 利用排除法，先判断函数的奇偶性，再根据函数的值域即可判断．

解答 解：∵f（-x）=${e}^{1-（-x）^{2}}$=f（x），
∴函数f（x）为偶函数，排除A，B，
∵$f（x）={e^{1-{x^2}}}$＞0，故排除D，
故选：C．

点评 本题考查了图象的识别，根据函数的奇偶性和函数的值域，是常用的方法，属于基础题．

练习册系列答案
相关题目
8．已知a，b，c∈R，a2+b2+c2=1．
（1）若a+b+c=0，求a的最大值．
（2）若ab+bc+ca的最大值为M，解不等式|x+1|+|x-1|≥3M．
9．若x∈R，则“2x＜1”是“-1＜x＜0”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
6．若$α∈（{\frac{π}{2}，π}），tanα=-\frac{1}{4}$，则sin（α+π）=-$\frac{\sqrt{17}}{17}$．
13．已知a＞0，x，y满足约束条件$\left\{\begin{array}{l}x≥1\\ x+y≤3\\ y≥a（{x-3}）.\end{array}\right.$，若z=2x+y的最小值为0，则a=1．
3．设变量x，y满足约束条件$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{y≥3}\end{array}\right.$，则目标函数z=x+3y的最小值为（　　）
A．-3B．0C．3D．12
10．已知$\frac{ai}{2-i}$+1=2i（i是虚数单位），则实数a=5．
7．有5个英语字母a、b、c、d、e排成一行，则a不排在正中间的位置，且b不排在两端的概率为$\frac{1}{2}$．
7．已知f（x）为定义在[0，2）上的函数，f（x）=$\left\{\begin{array}{l}{cosπx，x∈[0，\frac{1}{2}]}\\{\frac{1}{2}tan（πx+\frac{π}{2}），x∈（\frac{1}{2}，1）}\\{f（x-1），x∈[1，2）}\end{array}\right.$，则不等式f（2x-1）≤$\frac{1}{2}$的解集为（　　）
A．[$\frac{1}{3}，\frac{3}{4}$]∪[$\frac{4}{3}，\frac{7}{4}$]B．[$\frac{2}{3}，\frac{3}{4}$]∪[1，$\frac{7}{4}$]C．[$\frac{2}{3}，\frac{7}{8}$]∪[$\frac{7}{6}，\frac{11}{8}$]D．[$\frac{4}{3}，\frac{7}{4}$]∪[$\frac{7}{3}，\frac{11}{4}$]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网