题目内容
6.已知A(4,1,3),B(2,-5,1),C(3,7,-5),则平行四边形ABCD的顶点D的坐标是( )| A. | (2,4,-1) | B. | (2,3,1) | C. | (-3,1,5) | D. | (5,13,-3) |
分析 设出点D的坐标,利用向量的坐标运算与向量相等,列出方程组,即可求出点D的坐标.
解答 解:平行四边形ABCD中,设点D(x,y,z),
则$\overrightarrow{AB}$=(-2,-6,-2),$\overrightarrow{DC}$=(3-x,7-y,-5-z);
又$\overrightarrow{AB}$=$\overrightarrow{DC}$,
∴$\left\{\begin{array}{l}-2=3-x\\-6=7-y\\-2=-5-z\end{array}\right.$,
解得$\left\{\begin{array}{l}x=5\\ y=13\\ z=-3\end{array}\right.$;
∴点D的坐标为(5,13,-3).
故选:D.
点评 本题考查了空间向量的坐标运算与向量相等的应用问题.是基础题目.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
14.设等差数列{an}满足5a7=7a10,且a1>0,Sn为其前n项和,则Sn中最大的是( )
| A. | S16 | B. | S17 | C. | S18 | D. | S16或S17 |
11.点A,B在抛物线x2=2py(p>0)上,若AB的中点是(x0,y0),当直线AB的斜率存在时,其斜率为( )
| A. | $\frac{2p}{{y}_{0}}$ | B. | $\frac{p}{{y}_{0}}$ | C. | $\frac{p}{{x}_{0}}$ | D. | $\frac{{x}_{0}}{p}$ |
18.设log89=a,log35=b,则lg2=( )
| A. | $\frac{2}{2+3ab}$ | B. | $\frac{1-a}{2ab}$ | C. | $\frac{1-a}{a+2b}$ | D. | $\frac{1-a}{{a}^{2}+b}$ |
15.-700°是( )角.
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.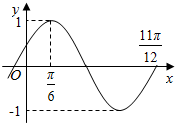 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,为了得到函数y=cos2x的图象,只需将函数y=f(x)的图象( )| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |