题目内容
8、设f（x）=x3+bx2+cx，又m是一个常数．已知当m＜0或m＞4时，f（x）-m=0只有一个实根；当0＜m＜4时，f（x）-m=0有三个相异实根，现给出下列命题：
（1）f（x）-4=0和f'（x）=0有一个相同的实根；
（2）f（x）=0和f'（x）=0有一个相同的实根；
（3）f（x）+3=0的任一实根大于f（x）-1=0的任一实根；
（4）f（x）+5=0的任一实根小于f（x）-2=0的任一实根．其中错误命题的个数是（ ）
（1）f（x）-4=0和f'（x）=0有一个相同的实根；
（2）f（x）=0和f'（x）=0有一个相同的实根；
（3）f（x）+3=0的任一实根大于f（x）-1=0的任一实根；
（4）f（x）+5=0的任一实根小于f（x）-2=0的任一实根．其中错误命题的个数是（ ）
分析：根据当m＜0或m＞4时，f（x）-m=0只有一个实根；当0＜m＜4时，f（x）-m=0有三个相异实根，得到0为函数的极小值，4为函数的极大值，根据题意可画出函数的大致图象，由图象可判断命题的真假．
解答：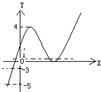
解：有题意可知4为f（x）=x3+bx2+cx的极大值，0为f（x）=x3+bx2+cx+d的极小值，
有右图，（1）（2）（4）正确．
故选D
解：有题意可知4为f（x）=x3+bx2+cx的极大值，0为f（x）=x3+bx2+cx+d的极小值，有右图，（1）（2）（4）正确．
故选D
点评：此题考查学生掌握利用导数研究函数极值的方法，灵活运用数形结合的数学思想解决数学问题，是一道基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设f（x）=x3+x2+x（x∈R），又若a∈R，则下列各式一定成立的是（ ）
| A、f（a）≤f（2a） | B、f（a2）≥f（a） | C、f（a2-1）＞f（a） | D、f（a2+1）＞f（a） |