题目内容
设f（x）=x3+ax2+bx+c，又k是一个常数，已知当k＜0或k＞4时，f（x）-k=0只有一个实根，当0＜k＜4时，f（x）-k=0有三个相异实根，则下列命题中错误的是（ ）
分析：因为函数是一元三次函数，所以是双峰函数，根据题目给出的函数在不同范围内实根的情况，画出函数f（x）的简图，然后借助于图象，逐一分析四个命题即可得到正确答案．
解答：解：因为f（x）=x3+ax2+bx+c，且f（x）-k=0在k＜0或k＞4时只有一个实数根，在0＜k＜4时有三个实数根，
所以其图象近似如下图，
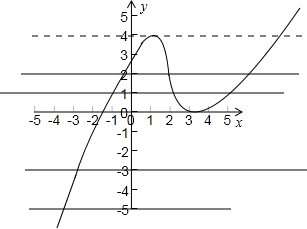
因为f′（x）=0的根是函数f（x）的极值点的横坐标，
由图象可知，f（x）-4=0和f′（x）=0有且只有一个相同的实根，所以命题（1）正确；
f（x）=0和f′（x）=0有且只有一个相同的实根，所以命题（2）正确；
f（x）+3=0的实根小于f（x）-1=0的实根，所以命题（3）不正确；
f（x）+5=0的实根小于f（x）-2=0的实根，所以命题（4）正确．
故选C．
所以其图象近似如下图，
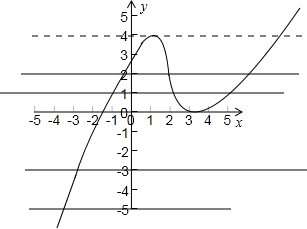
因为f′（x）=0的根是函数f（x）的极值点的横坐标，
由图象可知，f（x）-4=0和f′（x）=0有且只有一个相同的实根，所以命题（1）正确；
f（x）=0和f′（x）=0有且只有一个相同的实根，所以命题（2）正确；
f（x）+3=0的实根小于f（x）-1=0的实根，所以命题（3）不正确；
f（x）+5=0的实根小于f（x）-2=0的实根，所以命题（4）正确．
故选C．
点评：本题考查了命题的真假及应用，考查了利用导函数研究函数的极值，考查了数形结合的数学思想，解答此题的关键是能够根据方程f（x）-k=0的根的情况作出函数f（x）的图象的大致形状，此题是中挡题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
设f（x）=x3+bx+c是[-1，1]上的增函数，且f（-
）•f（
）＜0，则方程f（x）=0在[-1，1]内（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、可能有3个实数根 |
| B、可能有2个实数根 |
| C、有唯一的实数根 |
| D、没有实数根 |