题目内容
(本小题满分16分)
数列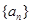 的前n项和为
的前n项和为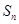 ,存在常数A,B,C,使得
,存在常数A,B,C,使得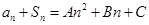 对任意正整数n都成立。
对任意正整数n都成立。
(1) 若数列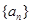 为等差数列,求证:3A-B+C=0;
为等差数列,求证:3A-B+C=0;
(2) 若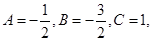 设
设 数列
数列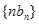 的前n项和为
的前n项和为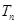 ,求
,求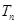 ;
;
(3) 若C=0,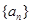 是首项为1的等差数列,设
是首项为1的等差数列,设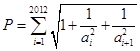 ,求不超过P的最大整数的值。
,求不超过P的最大整数的值。
数列
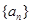 的前n项和为
的前n项和为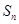 ,存在常数A,B,C,使得
,存在常数A,B,C,使得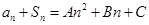 对任意正整数n都成立。
对任意正整数n都成立。(1) 若数列
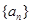 为等差数列,求证:3A-B+C=0;
为等差数列,求证:3A-B+C=0;(2) 若
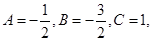 设
设 数列
数列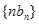 的前n项和为
的前n项和为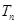 ,求
,求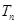 ;
;(3) 若C=0,
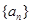 是首项为1的等差数列,设
是首项为1的等差数列,设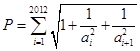 ,求不超过P的最大整数的值。
,求不超过P的最大整数的值。⑴见解析;⑵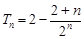 .⑶不超过
.⑶不超过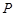 的最大整数为
的最大整数为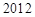 .
.
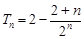 .⑶不超过
.⑶不超过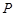 的最大整数为
的最大整数为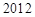 .
.本试题主要是考查了数列的通项公式的求解,以及数列的求和,和运用数列来证明不等式的综合运用。
(1)利用已知条件中通项公式和前n项和的关系式,得到前几项,结合等差数列的定义得到关系的证明。
(2)利用第一问的结论,表示数列的通项公式,分析特点,运用错位相减法等求解前n项和。
(3)根据等差数列得到需要求解的和式,得到结论。
解:⑴因为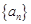 为等差数列,设公差为
为等差数列,设公差为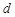 ,由
,由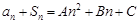 ,
,
得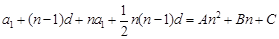 ,
,
即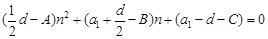 对任意正整数
对任意正整数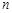 都成立.
都成立.
所以 所以
所以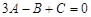 . ………………………………4分
. ………………………………4分
⑵ 因为 ,所以
,所以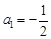 ,
,
当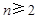 时,
时,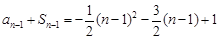 ,
,
所以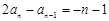 ,即
,即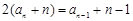 ,
,
所以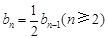 ,而
,而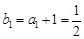 ,
,
所以数列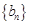 是首项为
是首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以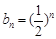 . ……………7分
. ……………7分
于是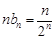 .所以
.所以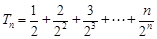 ①,
①, ,②
,②
由①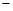 ②,
②,
得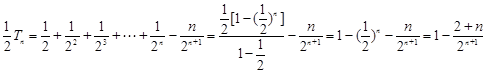 .
.
所以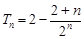 .…………………………………………………………………10分
.…………………………………………………………………10分
⑶ 因为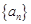 是首项为
是首项为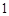 的等差数列,由⑴知,公差
的等差数列,由⑴知,公差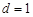 ,所以
,所以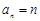 .
.
而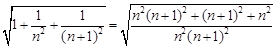
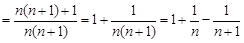 ,……………………………14分
,……………………………14分
所以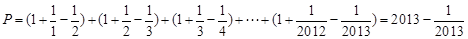 ,
,
所以,不超过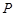 的最大整数为
的最大整数为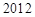 .………………………………………………16分
.………………………………………………16分
(1)利用已知条件中通项公式和前n项和的关系式,得到前几项,结合等差数列的定义得到关系的证明。
(2)利用第一问的结论,表示数列的通项公式,分析特点,运用错位相减法等求解前n项和。
(3)根据等差数列得到需要求解的和式,得到结论。
解:⑴因为
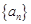 为等差数列,设公差为
为等差数列,设公差为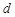 ,由
,由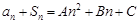 ,
,得
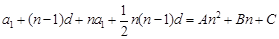 ,
,即
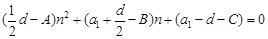 对任意正整数
对任意正整数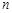 都成立.
都成立.所以
 所以
所以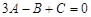 . ………………………………4分
. ………………………………4分⑵ 因为
 ,所以
,所以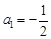 ,
,当
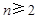 时,
时,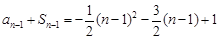 ,
,所以
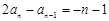 ,即
,即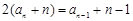 ,
,所以
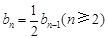 ,而
,而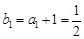 ,
,所以数列
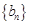 是首项为
是首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以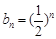 . ……………7分
. ……………7分于是
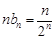 .所以
.所以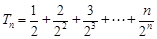 ①,
①, ,②
,②由①
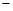 ②,
②,得
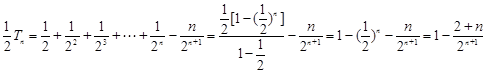 .
.所以
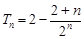 .…………………………………………………………………10分
.…………………………………………………………………10分⑶ 因为
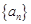 是首项为
是首项为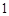 的等差数列,由⑴知,公差
的等差数列,由⑴知,公差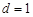 ,所以
,所以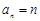 .
.而
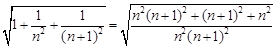
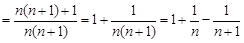 ,……………………………14分
,……………………………14分所以
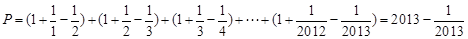 ,
,所以,不超过
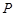 的最大整数为
的最大整数为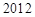 .………………………………………………16分
.………………………………………………16分
练习册系列答案
相关题目
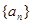 ,其前
,其前 项和为
项和为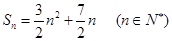 .
.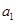 ,
,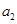 ;
;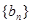 满足
满足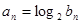 ,请证明数列
,请证明数列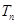 .
. 的通项是关于x的不等式
的通项是关于x的不等式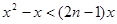
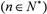 的解集中整数的个数.
的解集中整数的个数.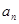 并且证明
并且证明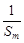 +
+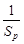 ≥
≥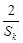 ;
;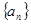 的首项
的首项 ,且满足
,且满足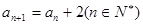 ,则数列
,则数列 ,且
,且 也成等差数列.
也成等差数列.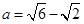 ,求⊿ABC的面积。
,求⊿ABC的面积。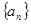 中,
中, ,且满足
,且满足 ,
,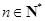 .
.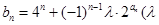 为非零整数,
为非零整数,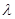 的值,使得对任意
的值,使得对任意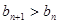 成立.
成立.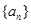 的前
的前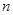 项和为
项和为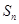 ,公比是正数的等比数列
,公比是正数的等比数列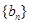 的前
的前 ,已知
,已知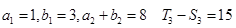
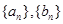 的通项公式。
的通项公式。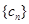 满足
满足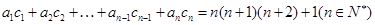 求数列
求数列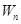 。
。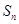 是数列
是数列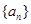 的前
的前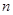 项和,且
项和,且
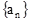 的通项公式;
的通项公式; 中,所有满足
中,所有满足 的正整数
的正整数 的个数称为这个数列
的个数称为这个数列 (n为正整数),求数列
(n为正整数),求数列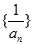 的前
的前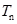 ,若
,若 对
对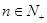 恒成立,求正整数
恒成立,求正整数 的最小值。
的最小值。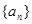 中,
中,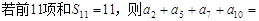 ( )
( )