题目内容
【题目】已知数列![]() 中,
中, ![]() ,前
,前![]() 项和
项和![]() 满足
满足![]() (
(![]() ).
).
⑴ 求数列![]() 的通项公式;
的通项公式;
⑵ 记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
⑶ 是否存在整数对![]() (其中
(其中![]() ,
, ![]() )满足
)满足![]() ?若存在,求出所有的满足题意的整数对
?若存在,求出所有的满足题意的整数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() ,
, ![]() ,
, ![]() .
.
【解析】试题分析: ![]() 当
当![]() 时,可得
时,可得![]() (
(![]() ),而当
),而当![]() 时,
时,
![]() (
(![]() ),可得到数列
),可得到数列![]() 是首项为
是首项为![]() ,公比也为
,公比也为![]() 的等比数列,从而可求数列
的等比数列,从而可求数列![]() 的通项公式;
的通项公式;
![]() 由
由![]() 知
知![]() ,代入
,代入![]() ,对通项公式进行裂项,即可求得数列
,对通项公式进行裂项,即可求得数列![]() 的前
的前![]() 项和
项和![]() ;
;
![]() 要求出所有的满足题意的整数对
要求出所有的满足题意的整数对![]() ,根据题目意思表达出
,根据题目意思表达出![]() 关于
关于![]() 的表达式,
的表达式,
![]() 然后进行讨论。
然后进行讨论。
解析:⑴ 当![]() 时,
时, ![]() 与
与![]() 相减,
相减,
得![]() ,即
,即![]() (
(![]() ),
),
在![]() 中,令
中,令![]() 可得,
可得, ![]() ,即
,即![]() ;
;
故![]() (
(![]() ),
),
故数列![]() 是首项为
是首项为![]() ,公比也为
,公比也为![]() 的等比数列,其通项公式为
的等比数列,其通项公式为![]() ;
;
⑵由⑴ 知, 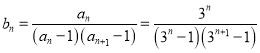
![]() ,
,
则![]() .
.
⑶![]() ,即
,即![]() ,
,
即![]() ,
,
若存在整数对![]() ,则
,则![]() 必须是整数,其中
必须是整数,其中![]() 只能是
只能是![]() 的因数,
的因数,
可得![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() ;
;
综上所有的满足题意得整数对为![]() ,
, ![]() ,
, ![]() .
.

练习册系列答案
相关题目
【题目】对某电子元件进行寿命追踪调查,情况如下.
寿命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
个 数 | 20 | 30 | 80 | 40 | 30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计元件寿命在100~400h以内的在总体中占的比例.