题目内容
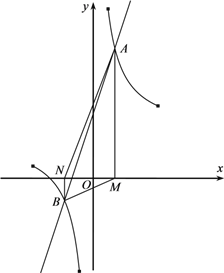
【题目】如图,已知直线![]() 与曲线
与曲线![]() 在第一象限和第三象限分别交于点
在第一象限和第三象限分别交于点![]() 和点
和点![]() ,分别由点
,分别由点![]() 、
、![]() 向
向![]() 轴作垂线,垂足分别为
轴作垂线,垂足分别为![]() 、
、![]() ,记四边形
,记四边形![]() 的面积为S.
的面积为S.
⑴ 求出点![]() 、
、![]() 的坐标及实数
的坐标及实数![]() 的取值范围;
的取值范围;
⑵ 当![]() 取何值时,S取得最小值,并求出S的最小值.
取何值时,S取得最小值,并求出S的最小值.
【答案】(1) 详见解析;(2)详见解析.
【解析】试题分析:(1)由题意得直线与曲线交两点,联立直线与曲线方程解得两点坐标,由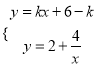 得,
得, ![]() 即
即![]() ,
, ![]() ,再由第一象限和第三象限求得
,再由第一象限和第三象限求得![]() 的取值范围(2)要求出S的最小值,将四边形沿
的取值范围(2)要求出S的最小值,将四边形沿![]() 轴分割成两个三角形,以
轴分割成两个三角形,以![]() 为公共底,
为公共底, ![]() 为高,表示出
为高,表示出![]() ,运用不等式求出结果
,运用不等式求出结果
解析:⑴ 由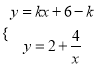 得,
得, ![]() ,
,
即![]() ,解得
,解得![]() 或
或![]() ,
,
![]() 当
当![]() 时,
时, ![]() ,即
,即![]() ,
,
当![]() 时,
时, ![]() ,即
,即![]() ,
,
![]() 点
点![]() 在第三象限,
在第三象限, 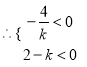 ,得
,得![]() ,
,
故![]() ,
, ![]() ,故实数
,故实数![]() 的取值范围为
的取值范围为![]() ;
;
⑵![]() ,则
,则![]() ,
,
![]() ,
,
∴![]() ,
,
故![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,
,
得![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
即四边形![]() 面积取得最小值8时,
面积取得最小值8时, ![]() .
.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
【题目】已知如表为“五点法”绘制函数f(x)=Asin(ωx+φ)图象时的五个关键点的坐标(其中A>0,ω>0,|φ|<π)
x | ﹣ |
|
|
|
|
f(x) | 0 | 2 | 0 | ﹣2 | 0 |
(Ⅰ)请写出函数f(x)的最小正周期和解析式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.