题目内容
【题目】偶函数 
= 
的图象过点 
,且在 
处的切线方程为 
.求 
的解析式．
【答案】
【解析】解：∵f(x)为偶函数,
∴b＝d＝0.
又图象过点P(0,1),则e＝1.
此时f(x)＝ax4＋cx2＋1.
∴y′＝4ax3＋2cx,
∴y′|x＝1＝4a＋2c＝1. ①
又切线的切点(1,-1)在曲线上,
∴a＋c＋1＝-1. ②
由①②得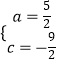 
,
∴f(x) ＝ 
x4- 
x2＋1.
所以答案是：
.
【考点精析】本题主要考查了函数的偶函数和导数的几何意义的相关知识点，需要掌握一般地，对于函数f(x)的定义域内的任意一个x，都有f(－x)=f(x)，那么f(x)就叫做偶函数；通过图像,我们可以看出当点
趋近于
时，直线
与曲线相切．容易知道，割线
的斜率是
，当点趋近于时，函数
在
处的导数就是切线PT的斜率k，即
才能正确解答此题．
练习册系列答案
相关题目
