题目内容
【题目】已知数列{an}满足:a1=1,|an+1-an|=pn,n∈N*,Sn为数列{an}的前n项和.
(1)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;
(2)若p=![]() ,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
(3)在(2)的条件下,令cn=n(an+1-an),求数列{cn}的前n项和Tn.
【答案】(1)p=![]() .(2)an=
.(2)an=![]() +
+![]() ·
·![]() .(3)
.(3)![]()
【解析】分析:(1)由题意得到关于p的方程,解方程可得p=![]() .
.
(2)由题意可知a2n+1-a2n-1>0,讨论可得a2n-a2n-1=![]() . 同理有a2n+1-a2n=
. 同理有a2n+1-a2n=![]() . 则数列的通项公式为an=
. 则数列的通项公式为an=![]() +
+![]() ·
·![]() .
.
(3)结合(2)中的结果首先求得数列![]() 的通项公式,然后求解其前n项和即可.
的通项公式,然后求解其前n项和即可.
详解:(1)因为{an}是递增数列,所以an+l-an=an+1-an=pn.
因为a1=1,a1,2a2,3a3成等差数列,所以4a2=a1+3a3,
则3a3-3a2=a2-a1,即3p2-p=0,解得p=![]() 或p=0.
或p=0.
当p=0时,an+1=an,这与{an}是递增数列矛盾,
所以p=![]() .
.
(2)由于{a2n-1}是递增数列,因而a2n+1-a2n-1>0,
所以(a2n+1-a2n)+(a2n-a2n-1)>0.
因为![]() <
<![]() ,所以a2n+1-a2n<a2n-a2n-1.
,所以a2n+1-a2n<a2n-a2n-1.
所以a2n-a2n-1>0,
因此a2n-a2n-1=(![]() )2n-1=
)2n-1=![]() .
.
因为{a2n}是递减数列,同理可得,a2n+1-a2n<0,
所以a2n+1-a2n=-(![]() )2n=
)2n=![]() .
.
所以an+1-an=![]() .
.
于是an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=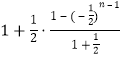 =1+
=1+![]() -
-![]() +…+
+…+![]() ,
,
所以数列{an}的通项公式为an=![]() +
+![]() ·
·![]() .
.
(3)由题意可知:![]()
![]()
![]() ,
,
则数列{cn}的前n项和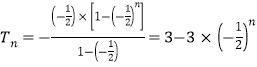 .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案