Question

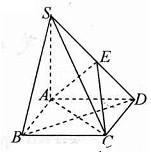如图，在底面是菱形的四棱锥S-ABCD中，SA=AB=2，SB=SD=2

2

．
（1）证明：BD⊥平面SAC；
（2）问：侧棱SD上是否存在点E，使得SB∥平面ACE？请证明你的结论．

Answer 1

分析：（1）根据四棱锥S-ABCD底面是菱形，得到BD⊥AC且AD=AB，又SA²+AB²=SB²，SA²+AD²=SD²，根据三边满足勾股定理可知SA⊥AB，SA⊥AD，又AB∩AD=A，根据线面垂直的判定定理可知SA⊥平面ABCD，而BD?平面ABCD，从而SA⊥BD，又SA∩AC=A，满足定理条件，BD⊥平面SAC；
（2）在侧棱SD上存在点E，使得SB∥平面ACE，其中E为SD的中点，然后证明，设BD∩AC=O，则O为BD的中点，又E为SD的中点，连接OE，则OE为△SBD的中位线，则OE∥SB，又OE?平面AEC，SB?平面AEC，根据线面平行的判定定理可知SB∥平面ACE．

解答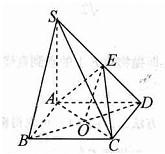：解：（1）∵四棱锥S-ABCD底面是菱形，∴BD⊥AC且AD=AB，
又SA=AB=2，SB=SD=2

2

．∴SA²+AB²=SB²，
SA²+AD²=SD²∴SA⊥AB，SA⊥AD，
又AB∩AD=A，∴SA⊥平面ABCD，
BD?平面ABCD，从而SA⊥BD
又SA∩AC=A，∴BD⊥平面SAC．

（2）在侧棱SD上存在点E，
使得SB∥平面ACE，其中E为SD的中点
证明如下：设BD∩AC=O，则O为BD的中点，
又E为SD的中点，连接OE，
则OE为△SBD的中位线．
∴OE∥SB，
又OE?平面AEC，SB?平面AEC
∴SB∥平面ACE

点评：本题主要考查了直线与平面垂直的判定，以及直线与平面平行的判定，同时考查了化归与转化的数学思想方法，以及空间想象能力、推理论证能力，属于中档题．