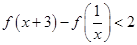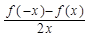题目内容
(本小题12分)
已知函数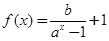
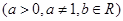 是奇函数,且
是奇函数,且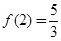
(1)求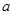 ,
,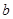 的值;
的值;
(2)用定义证明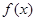 在区间
在区间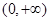 上是减函数.
上是减函数.
已知函数
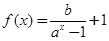
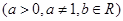 是奇函数,且
是奇函数,且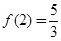
(1)求
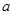 ,
,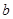 的值;
的值;(2)用定义证明
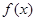 在区间
在区间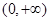 上是减函数.
上是减函数. (1)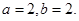 ;(2)见解析。
;(2)见解析。
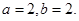 ;(2)见解析。
;(2)见解析。试题分析:(1)由题意知,
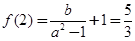 ,所以
,所以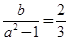 ①
①
因为函数
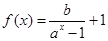 是奇函数,所以
是奇函数,所以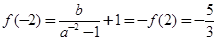 ,
,所以
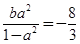 ②
②
由①②可得
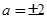 (
(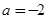 舍去),所以
舍去),所以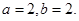
(2)由(1)可得
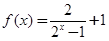 ,设
,设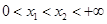 ,则
,则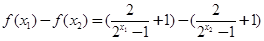
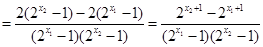
因为
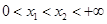 ,且
,且 在
在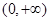 为增函数,
为增函数,所以
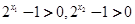 ,
,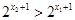 ,所以
,所以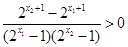 ,
,所以
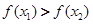 ,所以
,所以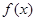 在区间
在区间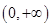 上是减函数
上是减函数 
点评:已知一个函数为奇函数,如果
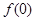 有意义,则
有意义,则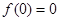 ,这个条件非常好用,常常能使运算变得非常简单;用定义法证明函数单调性时,要严格按照函数单调性的定义,遵循设变量、作差、变形、判断符号、下结论等步骤进行证明,另外需要注意的是变形时要化到最简单的形式,不要用已知函数的单调性来证明未知函数的单调性.用定义法证明函数的单调性是一个非常重要的考点,学生应该注意牢固掌握,灵活应用.
,这个条件非常好用,常常能使运算变得非常简单;用定义法证明函数单调性时,要严格按照函数单调性的定义,遵循设变量、作差、变形、判断符号、下结论等步骤进行证明,另外需要注意的是变形时要化到最简单的形式,不要用已知函数的单调性来证明未知函数的单调性.用定义法证明函数的单调性是一个非常重要的考点,学生应该注意牢固掌握,灵活应用.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
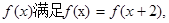 当
当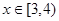 时,
时,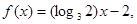 则
则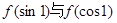 的大小关系为( )
的大小关系为( )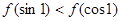
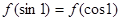
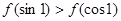
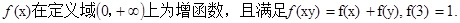
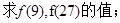
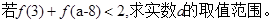
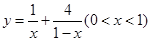 ,则
,则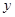 的最小值为 。
的最小值为 。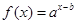 的图象如图所示,其中
的图象如图所示,其中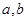 为常数,则下列结论正确的是
为常数,则下列结论正确的是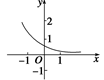
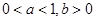
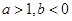
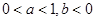
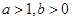
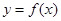 在区间
在区间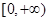 单调增加,则满足
单调增加,则满足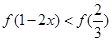 的
的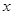 取值范围是( )
取值范围是( )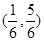
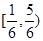
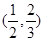
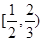
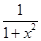 在(-∞,0)上的增减性.
在(-∞,0)上的增减性.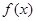 是定义在
是定义在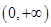 上的增函数,且
上的增函数,且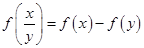
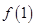 的值;(2)解不等式:
的值;(2)解不等式: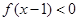 ;
;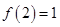 ,解不等式
,解不等式