题目内容
选修4-1：几何证明选讲如图，已知AB、CD是圆O的两条弦，且AB是线段CD的垂直平分线，已知AB=6，CD=2
| 5 |
分析：连接BC设AB，CD相交于点E，判断出AB是圆的直径．设AE=x，则EB=6-x，在直角三角形ACB中，由射影定理得CE2=AE•EB，得出关于x的方程并解出即可．
解答：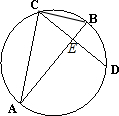
解：连接BC设AB，CD相交于点E，
设AE=x，
∵AB是线段CD的垂直平分线，
∴AB是圆的直径，∠ACB=90°…（2分）
则EB=6-x，CE=
．由射影定理得CE2=AE•EB，
即有x（6-x）=5，解得x=1（舍）或x=5…（8分）
∴AC2=AE•AB=5×6=30，即AC=
．…（10分）
解：连接BC设AB，CD相交于点E，设AE=x，
∵AB是线段CD的垂直平分线，
∴AB是圆的直径，∠ACB=90°…（2分）
则EB=6-x，CE=
| 5 |
即有x（6-x）=5，解得x=1（舍）或x=5…（8分）
∴AC2=AE•AB=5×6=30，即AC=
| 30 |
点评：本题考查与圆有关的比例线段，要善于寻找有关线段的数量关系，结合相关性质、定理求解．
练习册系列答案
相关题目
选修4-1：几何证明选讲
A、选修4-1：几何证明选讲 
选修4-1：几何证明选讲
（2012•徐州模拟）选修4-1：几何证明选讲
（2013•南京二模）选修4-1：几何证明选讲