题目内容
选修4-5:不等式选讲
已知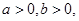 且
且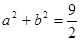 ,若
,若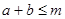 恒成立,
恒成立,
(Ⅰ)求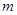 的最小值;
的最小值;
(Ⅱ)若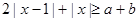 对任意的
对任意的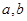 恒成立,求实数
恒成立,求实数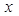 的取值范围.
的取值范围.
已知
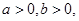 且
且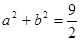 ,若
,若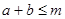 恒成立,
恒成立,(Ⅰ)求
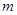 的最小值;
的最小值;(Ⅱ)若
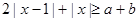 对任意的
对任意的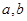 恒成立,求实数
恒成立,求实数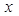 的取值范围.
的取值范围.(Ⅰ)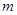 的最小值为
的最小值为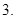 (Ⅱ)
(Ⅱ)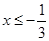 或
或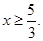
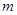 的最小值为
的最小值为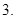 (Ⅱ)
(Ⅱ)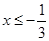 或
或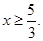
本试题主要是考查了绝对值不等式的求解,以及均值不等式的综合运用。
(1)因为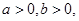 且
且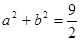 ,若
,若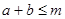 恒成立,只要求解a+b的最大值即可,利用
恒成立,只要求解a+b的最大值即可,利用
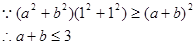 可知结论。
可知结论。
(2)由于要使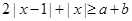 恒成立,须且只须
恒成立,须且只须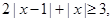 ,然后运用三段论的思想求解x的取值集合。
,然后运用三段论的思想求解x的取值集合。
解:(Ⅰ)
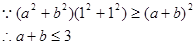
(当且仅当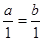 ,即
,即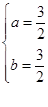 时取等号)
时取等号)
又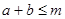 恒成立,
恒成立, 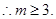
故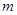 的最小值为
的最小值为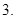 …………….4分
…………….4分
(Ⅱ)要使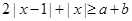 恒成立,须且只须
恒成立,须且只须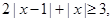
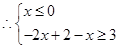 或
或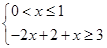 或
或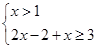
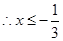 或
或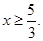 …………7分
…………7分
(1)因为
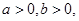 且
且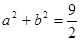 ,若
,若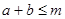 恒成立,只要求解a+b的最大值即可,利用
恒成立,只要求解a+b的最大值即可,利用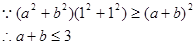 可知结论。
可知结论。(2)由于要使
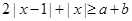 恒成立,须且只须
恒成立,须且只须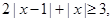 ,然后运用三段论的思想求解x的取值集合。
,然后运用三段论的思想求解x的取值集合。解:(Ⅰ)
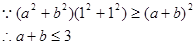
(当且仅当
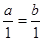 ,即
,即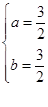 时取等号)
时取等号)又
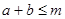 恒成立,
恒成立, 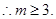
故
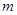 的最小值为
的最小值为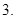 …………….4分
…………….4分(Ⅱ)要使
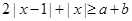 恒成立,须且只须
恒成立,须且只须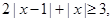
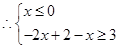 或
或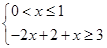 或
或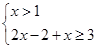
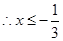 或
或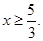 …………7分
…………7分
练习册系列答案
相关题目
 .
. ;
; 的不等式
的不等式 的解集不是空集,试求实数
的解集不是空集,试求实数 的取值范围.
的取值范围.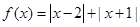
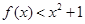 ;
;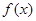 ≤
≤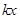 的解集为空集,求
的解集为空集,求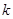 的取值范围。
的取值范围。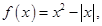 若
若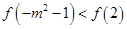 ,则实数
,则实数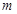 的取值范围
的取值范围 的最小值.
的最小值. 恒成立,求实数x的取值范围.
恒成立,求实数x的取值范围.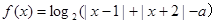 .
.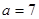 时,求函数
时,求函数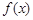 的定义域;
的定义域;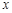 的不等式
的不等式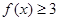 的解集是
的解集是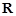 ,求实数
,求实数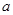 的取值范围.
的取值范围. 的解集为
的解集为 ,则实数
,则实数 __________.
__________.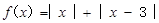 ,若f(x)
,若f(x)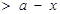 恒成立,则a的取值范围
恒成立,则a的取值范围