Question

【题目】已知定义在R上的函数对任意都有当时，则方程的解为_________.

Answer 1

【答案】

【解析】

由f（x+2）＝﹣f（x），可得函数f（x）是周期为4的周期函数．当-1≤x≤1时，求得f（x）的解，再根据函数的周期性即求函数f（x）的图象和直线y交点的横坐标，数形结合可得结论．

由f（x+2）＝﹣f（x），可得f（x+4）＝f（x），

故函数f（x）是周期为4的周期函数．

由于当﹣1≤x≤1时，f（x）x，

故当1≤x≤3时，有﹣1≤x﹣2≤1，

f（x）＝f[（x﹣2）+2]＝﹣f（x﹣2）（x﹣2）＝1x．

故有f（x）．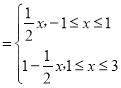

根据函数的周期性画出函数的图象，

根据题意可得，本题即求函数f（x）的图象和直线y交点的横坐标．

如图所示：数形结合可得函数f（x）的图象和直线y在上交点的横坐标为1，

则方程的解为

故答案为 ：