题目内容
下列命题的否定是真命题的是( )
| A.在△ABC中存在A>B,使sinA>sinB |
| B.空间中,任意两条没有公共点的直线都平行 |
| C.任意两个全等三角形的对应角相等 |
| D.?x、y∈R,x2+y2-4x+6y=0 |
对于A,在△ABC中,“A>B”,由于A+B<π,必有B<π-A
若A,B都是锐角,显然有“sinA>sinB”成立,
若A,B之一为锐角,必是B为锐角,此时有π-A不是钝角,由于A+B<π,必有B<π-A≤
,此时有sin(π-A)=sinA>sinB.所以A是正确命题.它的否定是假命题.
对于B,空间中异面直线也满足,任意两条直线没有公共点,所以B不正确.它的否定是真命题.
对于C,任意两个全等三角形的对应角相等,满足三角形全等的要求,所以C正确.它的否定是假命题.
对于D,?x、y∈R,x2+y2-4x+6y=0,显然x=y=0即可满足题意,所以D正确.
它的否定是假命题.
故选:B.
若A,B都是锐角,显然有“sinA>sinB”成立,
若A,B之一为锐角,必是B为锐角,此时有π-A不是钝角,由于A+B<π,必有B<π-A≤
| π |
| 2 |
对于B,空间中异面直线也满足,任意两条直线没有公共点,所以B不正确.它的否定是真命题.
对于C,任意两个全等三角形的对应角相等,满足三角形全等的要求,所以C正确.它的否定是假命题.
对于D,?x、y∈R,x2+y2-4x+6y=0,显然x=y=0即可满足题意,所以D正确.
它的否定是假命题.
故选:B.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
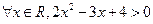 ; ②
; ②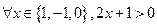 ;
;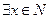 ,使
,使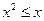 ; ④
; ④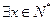 ,使
,使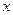 为29的约数.
为29的约数. 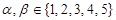 ,那么使得
,那么使得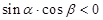 的数对
的数对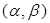 有 个.
有 个.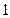 的整数只有两个正因数(1和它本身)”的否定是( )
的整数只有两个正因数(1和它本身)”的否定是( )