Question

4．正方形ABCD的边长为12，PA⊥平面ABCD，且PA=12，则点P到BD的距离为（　　）

• A． $6\sqrt{6}$
• B． 6$\sqrt{3}$
• C． $\sqrt{2}$
• D． 6$\sqrt{5}$

Answer 1

分析 连结AC交BD于0，由线面垂直的判定与性质证出BD⊥平面PAC，从而得到PO⊥BD，可得PO长就是点P到BD的距离．在Rt△PAO中，利用勾股定理算出PO，即可得到点P到BD的距离．

解答 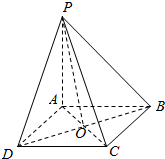解：连结AC交BD于0，
∵PA⊥平面ABCD，BD?平面ABCD，∴PA⊥BD
∵正方形ABCD中，AC⊥BD，
∴结合AC、PA是平面PAC内的相交直线，得BD⊥平面PAC
∵PO?平面PAC，
∴PO⊥BD，可得PO长就是点P到BD的距离
∵Rt△PAO中，PA=12cm，AO=$\frac{\sqrt{2}}{2}$AB=6$\sqrt{2}$
∴PO=$\sqrt{{PA}^{2}+{AO}^{2}}$=$\sqrt{{12}^{2}+（6\sqrt{2}）^{2}}$=6$\sqrt{6}$．
故选：A．

点评 本题经过正方形ABCD的顶点A作正方形所在平面的垂线，求垂线上一点P到正方形对角线BD的距离．着重考查了线面垂直的判定与性质、勾股定理和空间距离的求法等知识，属于中档题．