题目内容
20.若集合${M}=\left\{{y\left|{y=\frac{1}{x^2}}\right.}\right\}$,${N}=\left\{{x\left|{y=\sqrt{x-2}}\right.}\right\}$,那么 M∩N=( )| A. | (0,+∞) | B. | [0,+∞) | C. | (2,+∞) | D. | [2,+∞) |
分析 求出M中y的范围确定出M,求出N中x的范围确定出N,找出两集合的交集即可.
解答 解:由M中y=$\frac{1}{{x}^{2}}$>0,得到M=(0,+∞),
由N中y=$\sqrt{x-2}$,得到x-2≥0,即x≥2,
∴N=[2,+∞),
则M∩N=[2,+∞),
故选:D.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
8.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B,若椭圆上存在点P,使$\overrightarrow{PA}•\overrightarrow{PB}=0$,则椭圆离心率e的取值范围为( )
| A. | $[\frac{1}{2},1)$ | B. | $[\frac{{\sqrt{2}}}{2},1)$ | C. | $(0,\frac{{\sqrt{2}}}{2}]$ | D. | $[\frac{1}{2},\frac{{\sqrt{2}}}{2}]$ |
15.在等差数列{an}中,已知a4+a8=26,则该数列前11项和S11=( )
| A. | 58 | B. | 88 | C. | 143 | D. | 176 |
9.方程sin(x-2π)=lgx的实根有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无穷多个 |
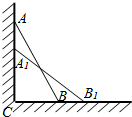 如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且AA1=($\sqrt{3}$-$\sqrt{2}$)米,则AB中点D所经过的路程为$\frac{π}{12}$米.
如图,一根木棒AB长为2米,斜靠在墙壁AC上,∠ABC=60°,若AB滑动至A1B1位置,且AA1=($\sqrt{3}$-$\sqrt{2}$)米,则AB中点D所经过的路程为$\frac{π}{12}$米.