题目内容
10.已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),若关于x的不等式f(x)<m的解集为(c,c+2$\sqrt{2}$).(1)求实数m的值;
(2)若x>1,y>0,x+y=m,求$\frac{1}{x-1}$+$\frac{2}{y}$的最小值.
分析 (1)根据函数的值域求出a与b的关系,然后根据不等式的解集可得x2+ax+$\frac{{a}^{2}}{4}$-m=0的两个根为c,c+2$\sqrt{2}$,2$\sqrt{m}$=c+2$\sqrt{2}$-c,解之即可.
(2)利用“1”的代换,即可求$\frac{1}{x-1}$+$\frac{2}{y}$的最小值.
解答 解:∵函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),
∴f(x)=x2+ax+b=0只有一个根,即△=a2-4b=0则b=$\frac{{a}^{2}}{4}$.
不等式f(x)<m的解集为(c,c+2$\sqrt{2}$).
即为x2+ax+$\frac{{a}^{2}}{4}$<m的解集为(c,c+2$\sqrt{2}$).
则x2+ax+$\frac{{a}^{2}}{4}$-m=0的两个根为c,c+2$\sqrt{2}$
∴2$\sqrt{m}$=c+2$\sqrt{2}$-c
∴m=2;
(2)x+y=2,∴x-1+y=1,
∴$\frac{1}{x-1}$+$\frac{2}{y}$=($\frac{1}{x-1}$+$\frac{2}{y}$)(x-1+y)=3+$\frac{y}{x-1}$+$\frac{2(x-1)}{y}$≥3+2$\sqrt{2}$.
当且仅当$\frac{y}{x-1}$=$\frac{2(x-1)}{y}$时,$\frac{1}{x-1}$+$\frac{2}{y}$的最小值为3+2$\sqrt{2}$.
点评 本题主要考查了一元二次不等式的应用,基本不等式的运用,同时考查了分析求解的能力和计算能力,属于中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
20.若集合${M}=\left\{{y\left|{y=\frac{1}{x^2}}\right.}\right\}$,${N}=\left\{{x\left|{y=\sqrt{x-2}}\right.}\right\}$,那么 M∩N=( )
| A. | (0,+∞) | B. | [0,+∞) | C. | (2,+∞) | D. | [2,+∞) |
1.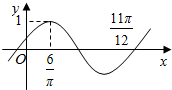 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$),f(x)的部分图象如图示,则关于y=f(x)错误的是( )| A. | 最小正周期为π | |
| B. | 向右平移$\frac{π}{6}$个单位得到函数y=sin(2x-$\frac{π}{6}$) | |
| C. | 在区间[0,$\frac{π}{2}$]上的值域为[-$\frac{1}{2},\frac{1}{2}$] | |
| D. | 向左平移$\frac{π}{6}$个单位得到的图象关于y轴对称 |
5.数列{an}满足a1=1,且对于任意的n∈N*都满足an+1=$\frac{{a}_{n}}{3{a}_{n}+1}$,则数列{anan+1}的前n项和为 ( )
| A. | $\frac{1}{3n+1}$ | B. | $\frac{n}{3n+1}$ | C. | $\frac{1}{3n-2}$ | D. | $\frac{n}{3n-2}$ |
19.已知定义在R上的奇函数f(x)满足f(x-2)=-f(x),则f(2006)的值为( )
| A. | 2006 | B. | 1003 | C. | 0 | D. | 不确定 |
 如图数表,为一组等式:某学生根据上表猜测S2n-1=(2n-1)(an2+bn+c),老师回答正确,则a-b+c=5.
如图数表,为一组等式:某学生根据上表猜测S2n-1=(2n-1)(an2+bn+c),老师回答正确,则a-b+c=5.