题目内容
13．已知定点A（2，0），动点M，N在y轴上滑动，且|MN|=4．（1）当M，N运动时，求△AMN外接圆的圆心C的轨迹方程；
（2）记∠MAN=θ，当θ最大时，求此时圆C的方程．
分析 （1）设圆心C（x，y），点C到y轴的距离为d，则d=|x|，利用勾股定理求动圆圆心C的轨迹方程；
（2）当θ最大时，OM=ON=2，求得圆心为（0，0），圆的半径为2，即可求出圆C的方程．
解答 解：（1）设圆心C（x，y），点C到y轴的距离为d，则d=|x|，
由勾股定理可得（x-2）2+y2=4+|x|2，
化简得y2=4x，即为所求轨迹方程．
（2）当θ最大时，OM=ON=2，∴圆心为（0，0），圆的半径为2，
圆的方程为x2+y2=4
点评 本题考查直线与圆的位置关系，考查圆的方程，属于中档题．
练习册系列答案
相关题目
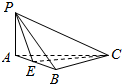如图，三棱锥P-ABC中，△PAB是正三角形，E是AB的中点，AB⊥BC，平面PAB⊥平面ABC．若AB=2，BC=$\sqrt{2}$，则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$．
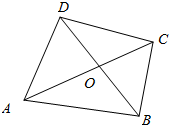如图所示，在四边形ABCD中，$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$，对角线AC与BD交于点O，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$．
15．若x≥1，a=（$\frac{1}{3}$）${\;}^{{x}^{2}+1}$，b=（$\frac{1}{3}$）x+1，c=（$\frac{1}{3}$）2x，则下列关系中正确的是（ ）
| A． | lga≥lgb≥1gc | B． | lgb≥lgc≥lga | C． | lgb≥lga≥lgc | D． | 1gc≥1ga≥lgb |