题目内容

函数f（x）=
ax+3，(x≤1)
1
x
+1，(x＞1)
，满足对任意定义域中的x1，x2（x1≠x2），[f（x1）-f（x2）]（x1-x2）＜0总成立，则实数a的取值范围是（　　）
A．（-∞，0）B．[-1，0）C．（-1，0）D．（-1，+∞），
∵对任意定义域中的x1，x2（x1≠x2），[f（x1）-f（x2）]（x1-x2）＜0总成立，
∴f（x）=
ax+3，(x≤1)
1
x
+1，(x＞1)
为定义域上的减函数，
作图如下：

∴
a＜0
a×1+3≥
1
1
+1
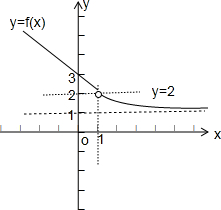
，即
a＜0
a≥-1
，
∴-1≤a＜0，
∴实数a的取值范围是[-1，0），
故选：B．
练习册系列答案
相关题目
已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=x3+x，则当x＜0时，f（x）=（　　）
A．f（x）=x3-xB．f（x）=-x3-xC．f（x）=-x3+xD．f（x）=x3+x
定义在R上的奇函数f（x）满足：f（x+1）=f（x-1），且当0≤x≤1时，f（x）=-8x2+8x，则f(-
2013
2
)=（　　）
A．2B．-1C．-2D．1
已知函数f（x）=a-
2
2x+1

（1）若f（x）为奇函数，求实数a的值；
（2）判断并证明f（x）的单调性．
下面有四个结论：
①偶函数的图象一定与y轴相交．
②奇函数的图象不一定过原点．
③偶函数若在（0，+∞）上是减函数，则在（-∞，0）上一定是增函数．
④有且只有一个函数既是奇函数又是偶函数．
其中正确结论的个数是（　　）
A．1B．2C．3D．4
已知函数f(x)=1-
2
3x+1
．
（1）求函数f（x）的定义域并判断函数f（x）的奇偶性；
（2）用单调性定义证明：函数f（x）在其定义域上都是增函数；
（3）解不等式：f（3m2-m+1）+f（2m-3）＜0．
定义在R上的偶函数y=f（x）在[0，+∞）上单调递减，函数f（x）的一个零点为
1
2
，则不等式f（log4x）＜0的解集是______．
已知函数f（x）=logax，（a＞0且a≠1）．
（1）若g（x）=f（|x|），当a＞1时，解不等式g（1）＜g（lgx）；
（2）若函数h（x）=|f（x-a）|-1，讨论h（x）在区间[2，4]上的最小值．
如果f（x）的图象关于y轴对称，而且在区间[0，+∞）为增函数，又f（-2）=0，那么（x-1）f（x）＜0的解集为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网