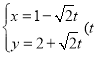题目内容
【题目】已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( )
A. [-3,6]
B. (-3,6)
C. (-∞,-3]∪[6,+∞)
D. (-∞,-3)∪(6,+∞)
【答案】D
【解析】
先求出导数f′(x),由f(x)有极大值、极小值可知f′(x)=0有两个不等实根.
函数f(x)=x3+ax2+(a+6)x+1,所以f′(x)=3x2+2ax+(a+6),
因为函数有极大值和极小值,所以方程f′(x)=0有两个不相等的实数根,
即3x2+2ax+(a+6)=0有两个不相等的实数根,
∴△>0,∴(2a)2﹣4×3×(a+6)>0,解得:a<﹣3或a>6.
故选:D.

练习册系列答案
相关题目