题目内容
(本题满分12分)已知函数 (其中
(其中 的最小正周期为
的最小正周期为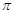 .
.
(Ⅰ)求 的值,并求函数
的值,并求函数 的单调递减区间;
的单调递减区间;
(Ⅱ)在锐角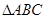 中,
中, 分别是角
分别是角 的对边,若
的对边,若
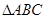 的面积为
的面积为 ,求
,求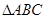 的外接圆面积.
的外接圆面积.
 (其中
(其中 的最小正周期为
的最小正周期为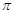 .
.(Ⅰ)求
 的值,并求函数
的值,并求函数 的单调递减区间;
的单调递减区间;(Ⅱ)在锐角
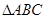 中,
中, 分别是角
分别是角 的对边,若
的对边,若
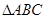 的面积为
的面积为 ,求
,求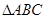 的外接圆面积.
的外接圆面积.(Ⅰ) ,
,
(Ⅱ)
 ,
,
(Ⅱ)

(I)先利用三角恒等变换公式把f(x)转化为 ,然后再根据周期确定出
,然后再根据周期确定出 的值,再利用正弦函数的单调增区间来求f(x)的单调减区间.
的值,再利用正弦函数的单调增区间来求f(x)的单调减区间.
(II)先由 求出
求出 ,再根据三角形的面积求出bc,再根据c值,求出b,再利用余弦定理求出a,根据正弦定理
,再根据三角形的面积求出bc,再根据c值,求出b,再利用余弦定理求出a,根据正弦定理 求出外接圆半径,从而求出
求出外接圆半径,从而求出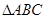 的外接圆面积.
的外接圆面积.
解:(Ⅰ)由已知得

于是有 …………(4分)
…………(4分)
 的单调递减区间为
的单调递减区间为 …(6分)
…(6分)
(Ⅱ)由(Ⅰ)及已知得
即 ,又
,又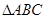 是锐角三角形,因此有
是锐角三角形,因此有


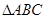 的外接圆半径等于
的外接圆半径等于
则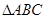 的外接圆面积等于
的外接圆面积等于 ……… (12分)
……… (12分)
 ,然后再根据周期确定出
,然后再根据周期确定出 的值,再利用正弦函数的单调增区间来求f(x)的单调减区间.
的值,再利用正弦函数的单调增区间来求f(x)的单调减区间.(II)先由
 求出
求出 ,再根据三角形的面积求出bc,再根据c值,求出b,再利用余弦定理求出a,根据正弦定理
,再根据三角形的面积求出bc,再根据c值,求出b,再利用余弦定理求出a,根据正弦定理 求出外接圆半径,从而求出
求出外接圆半径,从而求出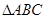 的外接圆面积.
的外接圆面积.解:(Ⅰ)由已知得


于是有
 …………(4分)
…………(4分) 的单调递减区间为
的单调递减区间为 …(6分)
…(6分)(Ⅱ)由(Ⅰ)及已知得

即
 ,又
,又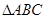 是锐角三角形,因此有
是锐角三角形,因此有


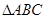 的外接圆半径等于
的外接圆半径等于
则
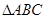 的外接圆面积等于
的外接圆面积等于 ……… (12分)
……… (12分)
练习册系列答案
相关题目
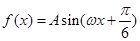 (其中
(其中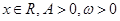 )的图象与
)的图象与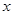 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为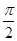 ,且图象上一个点为
,且图象上一个点为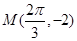 .
.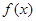 的解析式;
的解析式;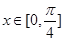 求函数
求函数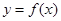 的图象向左平移
的图象向左平移 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的 解 析 式;
的 解 析 式; 中,角
中,角 的 对 边 分 别 是
的 对 边 分 别 是 ,若
,若 的 取 值 范 围.
的 取 值 范 围.
 上是增函数,
上是增函数, ,
,
 时,求
时,求 的值;
的值; 的最值以及
的最值以及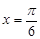 是函数
是函数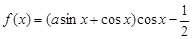 图象的一条对称轴.
图象的一条对称轴.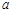 的值;
的值;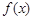 在
在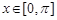 上的图象简图(不要求书写作图过程).
上的图象简图(不要求书写作图过程).
 ,函数
,函数
 ·
· ,
, .
. 的值;
的值; 
 ,求
,求 的值.
的值.  ,求函数f(x)的值域;
,求函数f(x)的值域; 的导函数
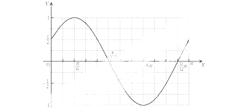
的导函数 的部分图像如图所示:图象与
的部分图像如图所示:图象与 轴交点
轴交点 ,与x轴正半轴的交点为A、C,B为图象的最低点 ,则函数
,与x轴正半轴的交点为A、C,B为图象的最低点 ,则函数

 中,若
中,若 ,求角
,求角 的大小.
的大小. 的图象按向量
的图象按向量 平移后,对应的函数为偶函数,求
平移后,对应的函数为偶函数,求 取最小值时的向量
取最小值时的向量 图象的一部分,则其函数解析式是( )
图象的一部分,则其函数解析式是( )



