题目内容
【题目】在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
证明DF⊥平面ABE;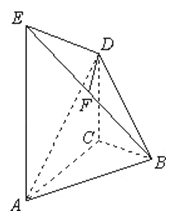
【答案】解:取AB的中点G,连接CG、FG.
因为CD∥AE,GF∥AE,所以CD∥GF.
又因为CD=1,![]() ,所以CD=GF.
,所以CD=GF.
所以四边形CDFG是平行四边形,DF∥CG.
在等腰Rt△ACB中,G是AB的中点,所以CG⊥AB.
因为EA⊥平面ABC,CG平面ABC,所以EA⊥CG.
而AB∩EA=A,所以CG⊥平面ABE.
又因为DF∥CG,所以DF⊥平面ABE.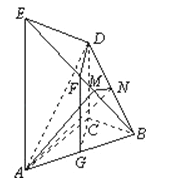
【解析】将DF平移到CG的位置,欲证DF⊥平面ABE,即证CG⊥平面ABE,根据线面垂直的判定定理可知,只需证CG与平面ABE内的两相交直线垂直即可;
【考点精析】解答此题的关键在于理解平面与平面之间的位置关系的相关知识,掌握两个平面平行没有交点;两个平面相交有一条公共直线.

练习册系列答案
相关题目

