题目内容
【题目】如图，已知抛物线x2=y，点A（﹣ 
， 
），B（ 
， 
），抛物线上的点P（x，y）（﹣ ＜x＜ ），过点B作直线AP的垂线，垂足为Q．
（Ⅰ）求直线AP斜率的取值范围；
（Ⅱ）求|PA||PQ|的最大值．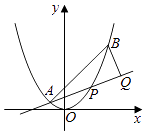
【答案】解：（Ⅰ）由题可知P（x，x2），﹣ 
＜x＜ 
，
所以kAP= 
=x﹣ ∈（﹣1，1），
故直线AP斜率的取值范围是：（﹣1，1）；
（Ⅱ）由（I）知P（x，x2），﹣ ＜x＜ ，
所以 
=（﹣ ﹣x， 
﹣x2），
设直线AP的斜率为k，则AP：y=kx+ k+ ，BP：y=﹣ 
x+ 
+ 
，
联立直线AP、BP方程可知Q（ 
， 
），
故 
=（ 
， 
），
又因为 =（﹣1﹣k，﹣k2﹣k），
故﹣|PA||PQ|= = 
+ 
=（1+k）3（k﹣1），
所以|PA||PQ|=（1+k）3（1﹣k），
令f（x）=（1+x）3（1﹣x），﹣1＜x＜1，
则f′（x）=（1+x）2（2﹣4x）=﹣2（1+x）2（2x﹣1），
由于当﹣1＜x＜﹣ 时f′（x）＞0，当 ＜x＜1时f′（x）＜0，
故f（x）max=f（ ）= 
，即|PA||PQ|的最大值为 ．
【解析】（Ⅰ）通过点P在抛物线上可设P（x，x2），利用斜率公式结合﹣ ＜x＜ 可得结论；
（Ⅱ）通过（I）知P（x，x2）、﹣ ＜x＜ ，设直线AP的斜率为k，联立直线AP、BP方程可知Q点坐标，进而可用k表示出 、 ，计算可知|PA||PQ|=（1+k）3（1﹣k），通过令f（x）=（1+x）3（1﹣x），﹣1＜x＜1，求导结合单调性可得结论．
【考点精析】本题主要考查了函数的最大(小)值与导数和斜率的计算公式的相关知识点，需要掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值；给定两点P1(x1,y1),P2(x2,y2),x1≠x2,用两点的坐标来表示直线P1P2的斜率：斜率公式: k=y2-y1/x2-x1才能正确解答此题．
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
