题目内容
(本小题满分12分)
如图,四棱锥P—ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD=2,
E、F分别为CD、PB的中点.
(1)求证:EF⊥平面PAB;
(2)设 求直线AC与平面AEF所成角
求直线AC与平面AEF所成角 的正弦值.
的正弦值.
如图,四棱锥P—ABCD中,底面ABCD为矩形,PD垂直于底面ABCD,AD=PD=2,
E、F分别为CD、PB的中点.
(1)求证:EF⊥平面PAB;
(2)设
 求直线AC与平面AEF所成角
求直线AC与平面AEF所成角 的正弦值.
的正弦值.
(1)证明见解析。
(2)
(2)
以D为从标原点,DC、DA、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系D—xyz.设AB=a,则A(0,2,0),B(a,2,0),
C(a,0,0),D(0,0,0,),p(0,0,2),
 …………2分
…………2分
(1)




 平面PAB. ………………6分
平面PAB. ………………6分
(2)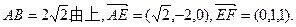
设平面AEF的法向量 ,
,
则
令y=1,则 …………9分
…………9分
又 …………11分
…………11分
 …………12分
…………12分
C(a,0,0),D(0,0,0,),p(0,0,2),
 …………2分
…………2分(1)





 平面PAB. ………………6分
平面PAB. ………………6分(2)
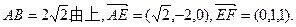
设平面AEF的法向量
 ,
,则

令y=1,则
 …………9分
…………9分又
 …………11分
…………11分 …………12分
…………12分
练习册系列答案
相关题目
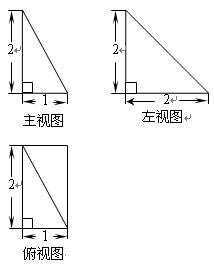
 的直观图和三视图如图所示,
的直观图和三视图如图所示, 是
是 的中点.
的中点. 是
是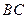 上任一点,求证:
上任一点,求证: ;
; ,
, 交于点
交于点 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
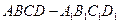 中,
中,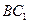 与对角面
与对角面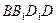 所成角的大小是________.
所成角的大小是________.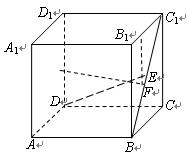

 沿对角线
沿对角线 折成直二面角,给出下列四个结论:①
折成直二面角,给出下列四个结论:① ;②
;② 与
与 所成角为
所成角为 ;③
;③ 为正三角形;④
为正三角形;④ 所成角为
所成角为



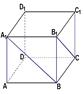
 的底面是边长为1的正方形,且侧棱垂直于底面,若
的底面是边长为1的正方形,且侧棱垂直于底面,若 与底面
与底面 成60°角,则二面角
成60°角,则二面角 的平面角的正切值为
的平面角的正切值为