题目内容
【题目】设等比数列{an}的前项n和Sn , a2= ![]() ,且S1+
,且S1+ ![]() ,S2 , S3成等差数列,数列{bn}满足bn=2n.
,S2 , S3成等差数列,数列{bn}满足bn=2n.
(1)求数列{an}的通项公式;
(2)设cn=anbn , 若对任意n∈N+ , 不等式c1+c2+…+cn≥ ![]() λ+2Sn﹣1恒成立,求λ的取值范围.
λ+2Sn﹣1恒成立,求λ的取值范围.
【答案】
(1)解:设数列{an}的公比为q,
∵ ![]() 成等差数列,∴
成等差数列,∴ ![]() ,∴
,∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]()
(2)解:设数列{cn}的前项n和为Tn,则Tn=c1+c2+c3+…+cn,
又 ![]() ,
,
∴ ![]() ,
, ![]() ,
,
两式相减得 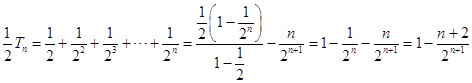 ,
,
∴ ![]() ,
,
又 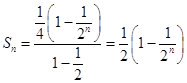 ,
,
∴对任意n∈N+,不等式 ![]() 恒成立等价于
恒成立等价于 ![]() 恒成立,
恒成立,
即 ![]() 恒成立,即
恒成立,即 ![]() 恒成立,
恒成立,
令 ![]() ,
, ![]() ,
,
∴f(n)关于n单调递减,∴ ![]() ,∴λ≤2,
,∴λ≤2,
∴λ的取值范围为(﹣∞,2]
【解析】(1)由S1+ ![]() ,S2 , S3成等差数列,可得
,S2 , S3成等差数列,可得 ![]() ,化简为
,化简为 ![]() ,又因为
,又因为 ![]() ,解得a1和q,即可求出等比数列{an}的通项公式;(2)因为{an}是等比数列,{bn}是等差数列,而cn=anbn , 故利用错位相减法即可求出Tn=c1+c2+…+cn , 将Tn和Sn代入不等式,并整理得
,解得a1和q,即可求出等比数列{an}的通项公式;(2)因为{an}是等比数列,{bn}是等差数列,而cn=anbn , 故利用错位相减法即可求出Tn=c1+c2+…+cn , 将Tn和Sn代入不等式,并整理得 ![]() ,记f(n)=
,记f(n)= ![]() ,
,
利用作差法可得f(n)关于n单调递减,则f(n)max=f(1)=1,故 ![]() ,即λ≤2.
,即λ≤2.

练习册系列答案
相关题目