题目内容
一个偶函数定义在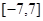 上,它在
上,它在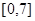 上的图象如图,下列说法正确的是( )
上的图象如图,下列说法正确的是( )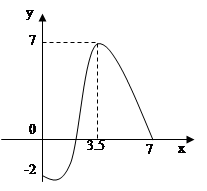
| A.这个函数仅有一个单调增区间 |
| B.这个函数有两个单调减区间 |
| C.这个函数在其定义域内有最大值是7 |
| D.这个函数在其定义域内有最小值是 -7 |
C
解析试题分析:根据偶函数在[0,7]上的图象及其对称性,作出在[-7,7]上的图象,如图所示,根据函数的图象,确定函数的单调性和最值情况,就可以确定选项。解:根据偶函数在[0,7]上的图象及其对称性,作出在[-7,7]上的图象,如图所示,可知:这个函数有三个单调增区间;这个函数有三个单调减区间;这个函数在其定义域内有最大值是7;这个函数在其定义域内最小值不是-7.故选C.
考点:函数的图像与性质
点评:本题主要考查了学生读图能力以及偶函数定义,本题关键是根据偶函数图象的对称性确定在[-7,7]上的图象,属于基础题.

练习册系列答案
相关题目
设函数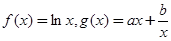 ,它们的图象在
,它们的图象在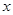 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当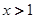 时,
时,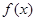 与
与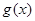 的大小关系是( )
的大小关系是( )
A.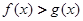 | B.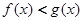 |
C.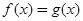 | D.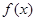 与 与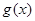 的大小不确定 的大小不确定 |
已知函数 ,
, ,且
,且 ,当
,当 时,
时, 是增函数,设
是增函数,设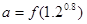 ,
,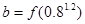 ,
, ,则
,则 、
、 、
、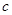 的大小顺序是( )。
的大小顺序是( )。
A. | B.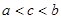 | C. | D. |
设函数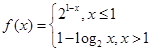 ,则满足
,则满足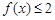 的
的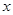 的取值范围是( )
的取值范围是( )
A.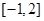 | B.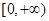 | C. | D.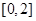 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D.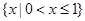 |
函数 在定义域
在定义域 内可导,其图像如图所示.记
内可导,其图像如图所示.记 的导函数为
的导函数为 ,则不等式
,则不等式 的解集为
的解集为 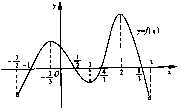
A.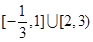 | B. |
C. | D.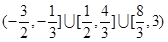 |
 ,若
,若 ,则
,则 =( )
=( )
A. | B. | C. | D. |
已知函数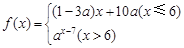 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( )
A.( ,1) ,1) | B.( , ,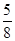 ) ) | C.( , ,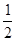 ) ) | D.(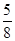 ,1) ,1) |
如果若干个函数的图象经过平移后能够重合,则称这些函数为“互为生成函数”。给出下列函数①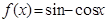 ;②
;②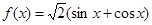 ;③
;③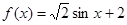 ;④
;④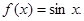 其中“互为生成函数”的是( )
其中“互为生成函数”的是( )
| A.①② | B.①③ | C.③④ | D.②④ |