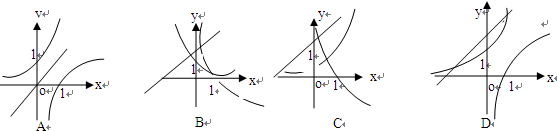
题目内容
设函数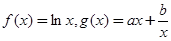 ,它们的图象在
,它们的图象在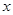 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当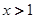 时,
时,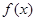 与
与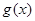 的大小关系是( )
的大小关系是( )
A.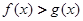 | B.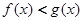 |
C.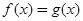 | D.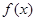 与 与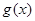 的大小不确定 的大小不确定 |
B
解析试题分析:f(x)与x轴的交点(1,0)在g(x)上,所以a+b=0,因为在此点有公切线,即此点导数相等,即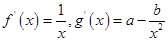 ,以上两式在x=1时相等,即1=a-b,又因为a+b=0,所以
,以上两式在x=1时相等,即1=a-b,又因为a+b=0,所以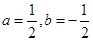 ,
,
即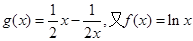 定义域{x|x>0},
定义域{x|x>0},
令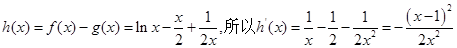 ,
,
∵x>1,∴h′(x)≤0,∴h(x)在(1,+∞)单调递减,即h(x)<0,∴f(x)<g(x)。故选B.
考点:导数的几何意义;利用导数研究曲线某点的切线方程;对数函数的图像和性质。
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及函数的基本性质,同时也考查了学生分析问题和解决问题的能力,属于中档题.

练习册系列答案
相关题目
当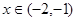 时,不等式
时,不等式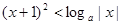 恒成立,则实数
恒成立,则实数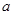 取值范围是( )
取值范围是( )
| A.[2,+∞) | B.(1,2] | C.(1,2) | D.(0,1) |
已知函数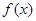 是
是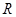 上的偶函数,且满足
上的偶函数,且满足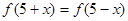 ,在[0,5]上有且只有
,在[0,5]上有且只有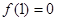 ,则
,则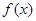 在[–2013,2013]上的零点个数为
在[–2013,2013]上的零点个数为
| A.808 | B.806 | C.805 | D.804 |
设函数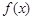
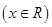 满足
满足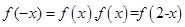 ,且当
,且当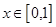 时,
时,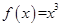 .又函数
.又函数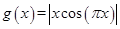 ,则函数
,则函数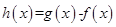 在
在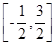 上的零点个数为( )
上的零点个数为( )
| A.5 | B.6 | C.7 | D.8 |
下列函数为奇函数,且在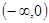 上单调递减的函数是( )
上单调递减的函数是( )
A.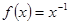 | B.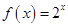 | C.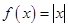 | D.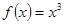 |
定义在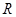 上的奇函数
上的奇函数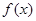 满足
满足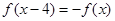 ,且在区间
,且在区间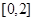 上是增函数,则( )
上是增函数,则( )
A. | B.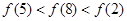 |
C.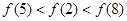 | D.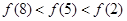 |
定义运算: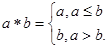 如
如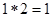 ,则函数
,则函数 的值域为( )
的值域为( )
A.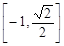 | B.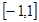 | C.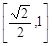 | D.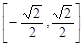 |
一个偶函数定义在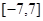 上,它在
上,它在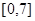 上的图象如图,下列说法正确的是( )
上的图象如图,下列说法正确的是( )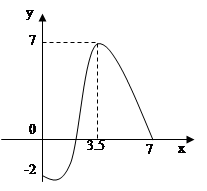
| A.这个函数仅有一个单调增区间 |
| B.这个函数有两个单调减区间 |
| C.这个函数在其定义域内有最大值是7 |
| D.这个函数在其定义域内有最小值是 -7 |
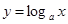 ,
,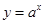 ,y=x+a的图象,可能正确的是
,y=x+a的图象,可能正确的是