题目内容
已知函数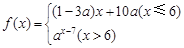 若数列{an}满足an=
若数列{an}满足an= (n∈N+)且{an}是递减数列,则实数a的取值范围是( )
(n∈N+)且{an}是递减数列,则实数a的取值范围是( )
A.( ,1) ,1) | B.( , ,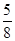 ) ) | C.( , ,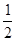 ) ) | D.(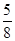 ,1) ,1) |
B
解析试题分析:由函数f(x),且数列{an}满足an=f(n)是递减数列,可得n≤6时,an=(1-3a)n+10,1-3a<0,且有最小值a6;n>6时,an=an-7,0<a<1,且有最大值a7;由a6>a7,得a的取值,从而得a的取值范围.
由函数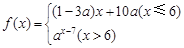 ,且数列{
,且数列{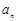 }满足an=f(n)是递减数列,则
}满足an=f(n)是递减数列,则
当n≤6时,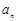 =(1-3a)n+10;则1-3a<0,∴a>
=(1-3a)n+10;则1-3a<0,∴a>
,且最小值a6=16-18a;
当n>6时,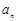 =
=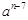 ;则0<a<1,且最大值
;则0<a<1,且最大值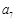 =1;
=1;
由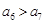 ,得16-18a>1,∴a<
,得16-18a>1,∴a<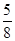 ;综上,知实数a的取值范围是:
;综上,知实数a的取值范围是: <a<
<a<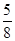 ;
;
故选B.
考点:数列与函数的综合
点评:本题考查了数列与分段函数的综合应用问题,解题时要认真分析,弄清题目中的数量关系,细心解答,以免出错.

练习册系列答案
相关题目
定义运算: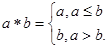 如
如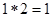 ,则函数
,则函数 的值域为( )
的值域为( )
A.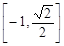 | B.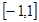 | C.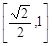 | D.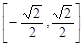 |
一个偶函数定义在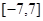 上,它在
上,它在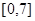 上的图象如图,下列说法正确的是( )
上的图象如图,下列说法正确的是( )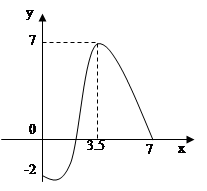
| A.这个函数仅有一个单调增区间 |
| B.这个函数有两个单调减区间 |
| C.这个函数在其定义域内有最大值是7 |
| D.这个函数在其定义域内有最小值是 -7 |
在用二分法求方程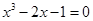 的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
的一个近似解时,现在已经将一根锁定在(1,2)内,则下一步可断定该根所在的区间为( )
| A.(1.4,2) | B.(1,1.4) | C.(1,1.5) | D.(1.5,2) |
已知 上是减函数,那么
上是减函数,那么 ( )
( )
| A.有最小值9 | B.有最大值9 | C.有最小值-9 | D.有最大值-9 |
若函数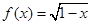 的定义域为A,函数
的定义域为A,函数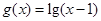 ,
,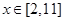 的值域为B,则
的值域为B,则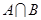 为
为
A.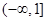 | B.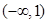 | C.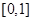 | D.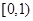 |
定义在R上的偶函数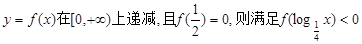 的x的集合为
的x的集合为
A.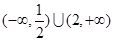 | B.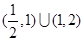 |
C.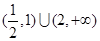 | D.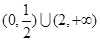 |
 的定义域是
的定义域是 ,则函数
,则函数 的定义域是 ( )
的定义域是 ( ) B.
B. 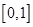 C.
C.  D.
D. 
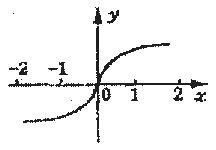
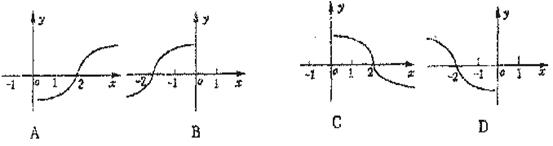
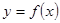 的曲线如图所示,那么方程
的曲线如图所示,那么方程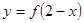 的曲线是( )
的曲线是( )