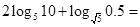题目内容
.已知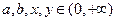 ,
,
(1)求证: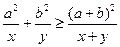 ,并指出等号成立的条件;
,并指出等号成立的条件;
(2)利用此不等式求函数 的最小值,并求出等号成立时的
的最小值,并求出等号成立时的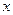 值.
值.
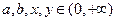 ,
,(1)求证:
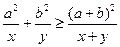 ,并指出等号成立的条件;
,并指出等号成立的条件;(2)利用此不等式求函数
 的最小值,并求出等号成立时的
的最小值,并求出等号成立时的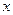 值.
值.解:(1)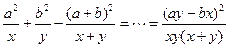
∵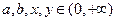 ∴
∴ 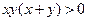 ,
,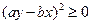
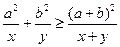 3分
3分
等号当且仅当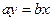 时成立 5分
时成立 5分
(2)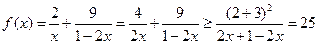 7分
7分
等号当且仅当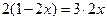 即
即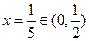 时成立 9分
时成立 9分
所以,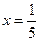 时,
时,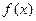 的最小值为
的最小值为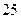 10分
10分
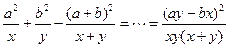
∵
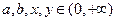 ∴
∴ 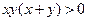 ,
,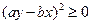
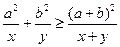 3分
3分等号当且仅当
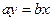 时成立 5分
时成立 5分(2)
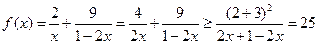 7分
7分等号当且仅当
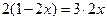 即
即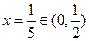 时成立 9分
时成立 9分所以,
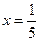 时,
时,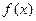 的最小值为
的最小值为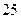 10分
10分略

练习册系列答案
相关题目
 是定义在R上的奇函数,且对任意a、b
是定义在R上的奇函数,且对任意a、b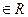 ,当
,当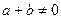 时,都有
时,都有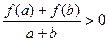 .
.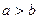 ,试比较
,试比较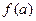 与
与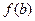 的大小关系;
的大小关系;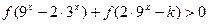 对任意
对任意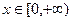 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.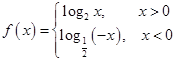 若
若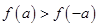 ,则实数
,则实数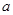 的取值范围是
的取值范围是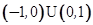
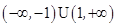
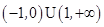
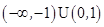
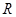 上的函数
上的函数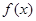 的图象是连续不断的,且有如下对应值表:
的图象是连续不断的,且有如下对应值表: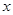
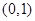 B、
B、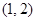 C、
C、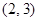 D、
D、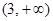
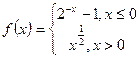 ,如果
,如果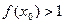 ,求
,求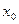 的取值范围.
的取值范围.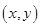 与B中元素
与B中元素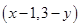 对应,则与B中元素
对应,则与B中元素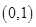 对应的A中元素是 ( )
对应的A中元素是 ( )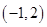
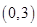
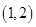
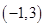
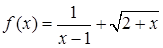 的定义域为
的定义域为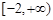
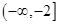
 R
R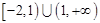
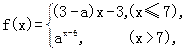 若x∈Z时,函数f(x)为递增函数,则实数a的取值范围为___________________
若x∈Z时,函数f(x)为递增函数,则实数a的取值范围为___________________