题目内容
【题目】记![]() 表示
表示![]() ,
,![]() 中的最大值,如
中的最大值,如![]()
![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上零点的个数;
上零点的个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() 个;(2)存在,
个;(2)存在,![]() .
.
【解析】
试题分析:(1)设![]() ,利用导数与单调性的关系求出
,利用导数与单调性的关系求出![]() ,可得
,可得![]() ,则
,则![]() ,结合图象可得零点的个数;(2)可将题意转化为
,结合图象可得零点的个数;(2)可将题意转化为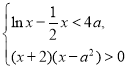 对
对![]() 恒成立,分别求
恒成立,分别求![]() 和
和![]() 成立即可.
成立即可.
试题解析:(1)设![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,![]() 递增;令
递增;令![]() ,得
,得![]() ,
,![]() 递减.
递减.
∴![]() ,∴
,∴![]() ,即
,即![]() ,∴
,∴![]() .
.
设![]() ,结合
,结合![]() 与
与![]() 在
在![]() 上图象可知,这两个函数的图象在
上图象可知,这两个函数的图象在![]() 上有两个交点,即
上有两个交点,即![]() 在
在![]() 上零点的个数为
上零点的个数为![]() .
.
(2)假设存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,
恒成立,
则 对
对![]() 恒成立,
恒成立,
即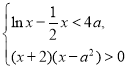 对
对![]() 恒成立,
恒成立,
(i)设![]() ,
,![]()
![]() ,
,
令![]() ,得
,得![]() ,
,![]() 递增;令
递增;令![]() ,得
,得![]() ,
,![]() 递减.
递减.
∴![]() .
.
当![]() ,即
,即![]() 时,
时,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
故当![]() 时,
时,![]() 对
对![]() 恒成立.
恒成立.
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上递减,∴
上递减,∴![]() .
.
∵![]() ,∴
,∴![]()
故当![]() 时,
时,![]() 对
对![]() 恒成立.
恒成立.
(ii)若![]() 对
对![]() 恒成立,则
恒成立,则![]() ,∴
,∴![]() .
.
由(i)及(ii)得,![]() .
.
故存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,
恒成立,
且![]() 的取值范围为
的取值范围为![]() .
.

【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
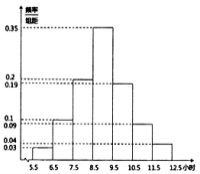
(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附:![]() (
(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】购买一辆某品牌新能源汽车,在行驶三年后,政府将给予适当金额的购车补贴.某调研机构对拟购买该品牌汽车的消费者,就购车补贴金额的心理预期值进行了抽样调查,其样本频率分布直方图如图所示
.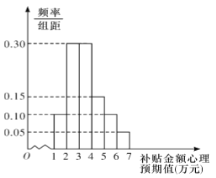
(1)估计拟购买该品牌汽车的消费群体对购车补贴金额的心理预期值的方差(同一组中的数据用该组区间的中点值作代表);
(2)将频率视为概率,从拟购买该品牌汽车的消费群体中随机抽取![]() 人,记对购车补贴金额的心理预期值高于
人,记对购车补贴金额的心理预期值高于![]() 万元的人数为
万元的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)统计最近![]() 个月该品牌汽车的市场销售量,得其频数分布表如下:
个月该品牌汽车的市场销售量,得其频数分布表如下:
月份 |
|
|
|
|
|
销售量(万辆) |
|
|
|
|
|
试预计该品牌汽车在![]() 年
年![]() 月份的销售量约为多少万辆?
月份的销售量约为多少万辆?
附:对于一组样本数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
,![]() .
.