题目内容
【题目】购买一辆某品牌新能源汽车，在行驶三年后，政府将给予适当金额的购车补贴.某调研机构对拟购买该品牌汽车的消费者，就购车补贴金额的心理预期值进行了抽样调查，其样本频率分布直方图如图所示
.
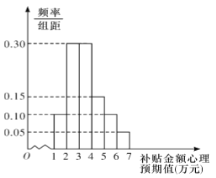
（1）估计拟购买该品牌汽车的消费群体对购车补贴金额的心理预期值的方差（同一组中的数据用该组区间的中点值作代表）；
（2）将频率视为概率，从拟购买该品牌汽车的消费群体中随机抽取
人，记对购车补贴金额的心理预期值高于
万元的人数为
，求的分布列和数学期望；
（3）统计最近
个月该品牌汽车的市场销售量，得其频数分布表如下：
月份 |
|
|
|
|
|
销售量（万辆） |
|
|
|
|
|
试预计该品牌汽车在
年月份的销售量约为多少万辆？
附：对于一组样本数据
，
，…，
，其回归直线
的斜率和截距的最小二乘估计分别为
，
.
【答案】（1）1.7；（2）
，见解析；（2）2.
【解析】
（1）平均数的估计值为每个小矩形组中值乘以小矩形面积的和；
（2）易得
，由二项分布列的期望公式计算；
（3）利用所给公式计算出回归直线
即可解决.
（1）由频率分布直方图可知，消费群体对购车补贴金额的心理预期值的平均数的估计值为
，所以方差的估计
值为
；
（2）由频率分布直方图可知，消费群体对购车补贴金额的心理预期值高于3万元的
频率为
，则，所以
的分布列为
，数学期望
；
（3）将 2018年11月至2019年3月的月份数依次编号为 1，2，3，4，5，
记 
，
，
，
，
，
，由 散 点 图可知，
5组样本数据呈线性相关关系，因为
，
，
，
，则
，
，
所以回归直线方程为
，当
时，
，预计该品
牌汽车在
年
月份的销售量约为2万辆.
练习册系列答案
相关题目
