题目内容
【题目】设不等式组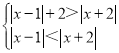
的解集为M，且a，b∈M．
（1）证明：|a+3b|＜2
（2）试比较|1﹣4ab|与2|a﹣b|的大小，并说明理由
【答案】（1）见解析（2）|1﹣4ab|＞2|a﹣b|．见解析
【解析】
(1)分段去绝对值,再求解分段函数的不等式求解
,再根据三角不等式证明即可.
(2)将
与
平方后作差比较大小即可.
（1）令f（x）＝|x﹣1|﹣|x+2|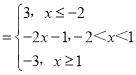
,
由题意可得﹣2＜|x﹣1|﹣|x+2|＜0,即﹣2＜﹣2x﹣1＜0,解得
；
则M＝{x|}；
∴|a+3b|≤|a|+3|b|
；
∴原题得证．
（2）由（1）可得
；
∵|1﹣4ab|2﹣4|a﹣b|2
＝（1﹣8ab+16a2b2）﹣4（a2﹣2ab+b2）
＝（4a2﹣1）（4b2﹣1）＞0,
∴|1﹣4ab|2＞4|a﹣b|2,
故|1﹣4ab|＞2|a﹣b|．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
