Question

（2013•宁波二模）三个顶点均在椭圆上的三角形称为椭圆的内接三角形．已知点A是椭圆的一个短轴端点，如果以A为直角顶点的椭圆内接等腰直角三角形有且仅有三个，则椭圆的离心率的取值范围是（　　）

• A．(0，

  2

  2

  )
• B．(

  2

  2

  ，

  6

  3

  )
• C．(

  2

  2

  ，1)
• D．(

  6

  3

  ，1)

Answer 1

分析：设椭圆的方程为

x2

a2

+

y2

b2

=1，直线AB方程为y=kx+b（k＞0），两方程联解得到B的横坐标为-

2ka2b

a2k2+b2

，从而得|AB|=

1+k2

•

2ka2b

a2k2+b2

，同理得到|AC|=

1+ 1 k2

•

2ka2b

b2k2+a2

．根据|AB|=|AC|建立关于k、a、b的方程，化简整理得到（k-1）[b²k²+（b²-a²）k+b²]=0，结合题意得该方程有三个不相等的实数根，根据一元二次方程根与系数的关系和根的判别式建立关于a、b的不等式，解之即得c²＞2b²，由此结合a²=b²+c²即可解出该椭圆的离心率的取值范围．

解答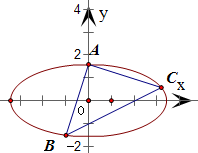：解：设椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），
根据BA、AC互相垂直，设直线AB方程为y=kx+b（k＞0），AC方程为y=-

1

k

x+b
由

x2 a2 + y2 b2 =1 y=kx+b

，消去y并化简得（a²k²+b²）x²+2ka²bx=0
解之得x₁=0，x₂=-

2ka2b

a2k2+b2

，可得B的横坐标为-

2ka2b

a2k2+b2

，
∴|AB|=

1+k2

|x₁-x₂|=

1+k2

•

2ka2b

a2k2+b2

．
同理可得，|AC|=

1+ 1 k2

•

2ka2b

b2k2+a2

∵△ABC是以A为直角顶点的椭圆内接等腰直角三角形，
∴|AB|=|AC|即

1+k2

•

2ka2b

a2k2+b2

=

1+ 1 k2

•

2ka2b

b2k2+a2

，
化简整理，得b²k³-a²k²+a²k-b²=0，分解因式得：（k-1）[b²k²+（b²-a²）k+b²]=0…（*）
方程（*）的一个解是k₁=1，另两个解是方程b²k²+（b²-a²）k+b²=0的根
∵k₁=1不是方程b²k²+（b²-a²）k+b²=0的根，
∴当方程b²k²+（b²-a²）k+b²=0有两个不相等的正数根时，方程（*）有3个不相等的实数根
相应地，以A为直角顶点的椭圆内接等腰直角三角形也有三个．
因此，△=（b²-a²）²-2b⁴＞0且

k2+k3= a2-b2 b2 ＞0 k1k2= b2 b2 ＞0

，化简得c²＞2b²
即3c²＞2a²，两边都除以3a²得

c2

a2

＞

2

3

，
∴离心率e满足e²＞

2

3

，解之得e＞

6

3

，结合椭圆的离心率e＜1，得

6

3

＜e＜1
故选：D

点评：本题给出以椭圆上顶点为直角顶点的内接等腰直角三角形存在3个，求椭圆的离心率取值范围，着重考查了椭圆的标准方程、简单几何性质和直线与椭圆位置关系等知识点，属于中档题．