Question

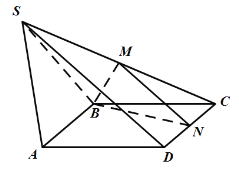
【题目】如图，正方形ADEF与梯形ABCD所在平面互相垂直，，，点M是EC的中点．

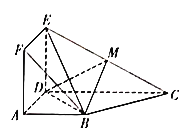
(1)求证:平面ADEF平面BDE.

(2)求二面角的余弦值.

Answer 1

【答案】(1)见证明；(2)

【解析】

(1)由勾股定理可得BD⊥AD，再利用面面垂直的性质可得ED⊥BD，结论得证；

（2）建立直角坐标系，分别求出平面BDE和平面BDM的法向量，利用空间向量求其二面角可得答案.

解：(1)由题可知AD=BD=2，AB=则AD2+BD2=AB，

根据勾股定理有BD⊥AD，

又因正方形ADEF 与梯形ABCD所在平面互相垂直，则ED⊥平面ABCD，

则ED⊥BD，而AD∩ED=D，所以BD⊥平面ADEF.

而BD平面BDE，所以平面ADEF⊥平面BDE.

(2)以D为坐标原点，分别以DA，DB，DE为x轴，y轴，z轴建立空间直角坐标系，

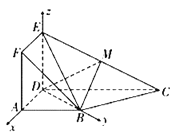
由题可得D（0，0，0），A（2，0，0），B（0.2，0），E（0，0，2），C（-2，2，0），M（-，，1）.

由(1)可得AD⊥平面BDE，则可取平面BDE的法向量，设平面BDM的法向量为，=（-，，1），=（0，2，0），

由·=0，·=0，.可得

可取=（，0，2），则.

设二面角E-BD-M的平面角为α，显然α为锐角，

故