题目内容
已知函数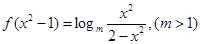 .
.
(1)判断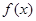 的奇偶性;
的奇偶性;
(2)求满足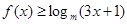 的
的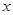 的取值范围.
的取值范围.
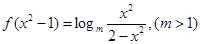 .
.(1)判断
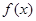 的奇偶性;
的奇偶性;(2)求满足
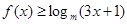 的
的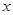 的取值范围.
的取值范围. (1) 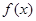 为奇函数 (2)
为奇函数 (2)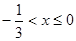 或
或
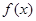 为奇函数 (2)
为奇函数 (2)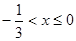 或
或
本试题主要是考查了函数的奇偶性和函数与不等式的关系的综合运用。
(1)由条件知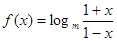 ,
,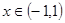 ,所以,
,所以,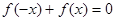 ,
,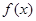 为奇函数
为奇函数
(2)解不等式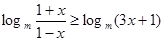 ,由于
,由于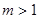 ,得到
,得到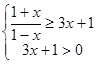 ,求解得到结论
,求解得到结论
(1)由条件知
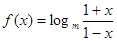 ,
,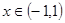 ,所以,
,所以,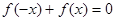 ,
,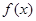 为奇函数
为奇函数(2)解不等式
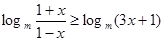 ,由于
,由于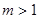 ,得到
,得到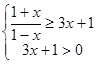 ,求解得到结论
,求解得到结论
练习册系列答案
相关题目
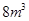 ,深为
,深为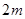 的长方体无盖水池,如果池底和池壁的造价分别为每平方米120元和80元,那么水池的最低总造价是多少元?
的长方体无盖水池,如果池底和池壁的造价分别为每平方米120元和80元,那么水池的最低总造价是多少元?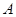 到
到 的映射
的映射 ,那么集合
,那么集合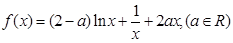
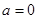 时,求
时,求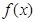 的极值;
的极值;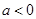 时,求
时,求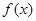 的定义域为
的定义域为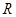 ,
,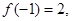 对任意
对任意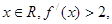 则
则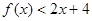 的解集为( )
的解集为( )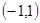
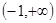
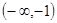
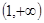
 ,其导函数为
,其导函数为 .
. 的单调减区间是
的单调减区间是 ;
; ;
; 时,对任意的
时,对任意的 且
且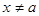 ,恒有
,恒有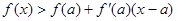

 ,
,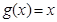
 ,
,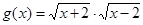
 ,
,
 ,
,
 地和
地和 地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知
地同时开出,如下图,各沿箭头方向(两方向垂直)匀速前进,汽车和自行车的速度分别是10米/秒和5米/秒,已知 米.(汽车开到
米.(汽车开到 秒后,汽车到达
秒后,汽车到达 处,自行车到达
处,自行车到达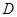 处,设
处,设 间距离为
间距离为 ,试写出
,试写出