题目内容
【题目】水是地球上宝贵的资源,由于介个比较便宜在很多不缺水的城市居民经常无节制的使用水资源造成严重的资源浪费.某市政府为了提倡低碳环保的生活理念鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x(吨),一位居民的月用水量不超过x的部分按平价收费,超出x的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[1,1.5),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图. 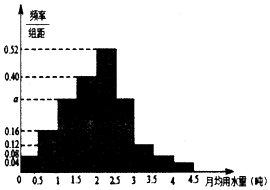
(1)若全市居民中月均用水量不低于3吨的人数为3.6万,试估计全市有多少居民?并说明理由;
(2)若该市政府拟采取分层抽样的方法在用水量吨数为[1,1.5)和[1.5,2)之间选取7户居民作为议价水费价格听证会的代表,并决定会后从这7户家庭中按抽签方式选出4户颁发“低碳环保家庭”奖,设X为用水量吨数在[1,1.5)中的获奖的家庭数,Y为用水量吨数在[1.5,2)中的获奖家庭数,记随机变量Z=|X﹣Y|,求Z的分布列和数学期望.
【答案】
(1)解:由图,不低于3吨人数所占百分比为0.5×(0.12+0.08+0.04)=12%,
所以假设全市的人数为x(万人),则有0.12x=3.6,解得x=30,
所以估计全市人数为30万
(2)解:由概率统计相关知识,各组频率之和的值为1,
因为频率= ![]() ,
,
所以0.5×(0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a)=1,得a=0.3,
用水量在[1,1.5]之间的户数为100×0.3×0.5=15户,
而用水量在[1.5,2]吨之间的户数为100×0.4×0.5=20户,
根据分层抽样的方法,总共需要抽取7户居民,
所以用水量在[1,1.5]之间应抽取的户数为 ![]() 户,
户,
而用水量在[1.5,2]吨之间的户数为 ![]() 户.
户.
据题意可知随机变量Z的取值为0,2,4. ![]() ,
, ![]() ,
, ![]() ,
,
其分布列为:
Z | 0 | 2 | 4 |
P |
|
|
|
期望为:E(Z)=0× ![]() +2×
+2× ![]() +
+ ![]() =
= ![]()
【解析】(1)由图,不低于3吨人数所占百分比为0.5×(0.12+0.08+0.04)=12%,解出即可得出.(2)由概率统计相关知识,各组频率之和的值为1,频率= ![]() ,可得0.5×(0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a)=1,得a.据题意可知随机变量Z的取值为0,2,4.利用相互独立、互斥事件的概率计算公式即可得出.
,可得0.5×(0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a)=1,得a.据题意可知随机变量Z的取值为0,2,4.利用相互独立、互斥事件的概率计算公式即可得出.
【考点精析】关于本题考查的频率分布直方图和离散型随机变量及其分布列,需要了解频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能得出正确答案.

 阅读快车系列答案
阅读快车系列答案