题目内容
【题目】已知菱形 ABCD 中,对角线 AC 与 BD 相交于一点 O,∠A=60°,将△BDC 沿着 BD 折起得△BDC',连结 AC'.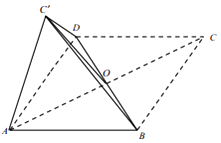
(Ⅰ)求证:平面 AOC'⊥平面 ABD;
(Ⅱ)若点 C'在平面 ABD 上的投影恰好是△ABD 的重心,求直线 CD 与底面 ADC'所成角的正弦值.
【答案】解:(Ⅰ)∵C′O⊥DB,AO⊥BD,C′O∩AO=O,∴BD⊥面 AOC',
又BD平面 ABD,∴平面 AOC'⊥平面 ABD.
(Ⅱ)如图建立空间直角坐标系O﹣xyz,

令AB=a,则A( ![]() ,0,0).
,0,0).
B(0, ![]() ,0),D(0,﹣
,0),D(0,﹣ ![]() ,0),C′(
,0),C′( ![]() ),
),
设面ADC'的法向量为 ![]()
![]() ,
, ![]() ,
, ![]()
由  可取
可取 ![]()
![]()
∴直线 CD 与底面 ADC'所成角的正弦值为: ![]()
【解析】(Ⅰ)只需证明C′O⊥DB,AO⊥BD,C′O∩AO=O,BD⊥面 AOC',即可得平面 AOC'⊥平面 ABD;
(Ⅱ)如图建立空间直角坐标系O﹣xyz,令AB=a,则A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),D(0,﹣
,0),D(0,﹣ ![]() ,0),C′(
,0),C′( ![]() , 0 ,
, 0 ,![]() ),利用向量法求解。
),利用向量法求解。
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下面是某日水深的数据:
t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y/m | 10 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 10 |
经长期观察,y=f(t)的曲线可以近似地看成函数![]() 的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).
(1)求y与t满足的函数关系式;
(2)某船吃水深度(船底离水面的距离)为6.5m,如果该船希望在同—天内安全进出港,请问该船在什么时间段能够安全进港?它同一天内最多能在港内停留多少小时?(忽略进 出港所需的时间).