题目内容
某单位有 、
、 、
、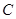 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为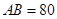
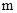 ,
,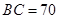
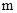 ,
,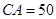
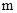 .假定
.假定 、
、 、
、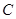 、
、 四点在同一平面上.
四点在同一平面上.
(1)求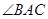 的大小;
的大小;
(2)求点 到直线
到直线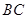 的距离.
的距离.
(1)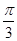 ;(2)
;(2)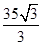 m
m
解析试题分析:(1)先确定 的三条边长,然后利用余弦定理求
的三条边长,然后利用余弦定理求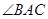 的大小;(2)方法1:先利用点
的大小;(2)方法1:先利用点 到三点
到三点 、
、 、
、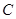 的距离相等将点
的距离相等将点 视为
视为 外接圆的圆心,利用正弦定理先算出
外接圆的圆心,利用正弦定理先算出 外接圆的半径,然后再构造直角三角形借助勾股定理计算点
外接圆的半径,然后再构造直角三角形借助勾股定理计算点 到直线
到直线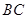 的距离;方法2:先利用点
的距离;方法2:先利用点 到三点
到三点 、
、 、
、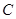 的距离相等将点
的距离相等将点 视为
视为 外接圆的圆心,直接利用锐角三角函数计算点
外接圆的圆心,直接利用锐角三角函数计算点 到直线
到直线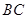 的距离.
的距离.
试题解析:方法1:因为发射点 到
到 、
、 、
、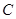 三个工作点的距离相等,
三个工作点的距离相等,
所以点 为△
为△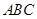 外接圆的圆心. 5分
外接圆的圆心. 5分
设外接圆的半径为 ,
,
在△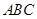 中,由正弦定理得
中,由正弦定理得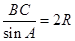 , 7分
, 7分
因为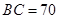 ,由(1)知
,由(1)知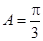 ,所以
,所以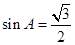 .
.
所以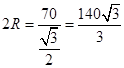 ,即
,即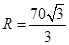 . 8分
. 8分
过点 作边
作边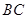 的垂线,垂足为
的垂线,垂足为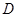 , 9分
, 9分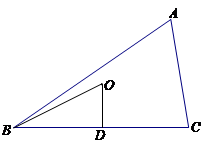
在△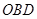 中,
中,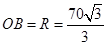 ,
,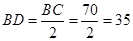 ,
,
所以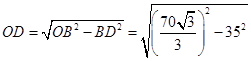 11分
11分 .
.
所以点 到直线
到直线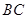 的距离为
的距离为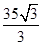
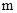 . 12分
. 12分
方法2:因为发射点 到
到 、
、 、
、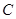 三个工作点的距离相等,
三个工作点的距离相等,
所以点 为△
为△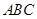 外接圆的圆心. 5分
外接圆的圆心. 5分
连结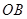 ,
,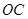 ,
,
过点 作边
作边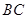 的垂线,垂足为
的垂线,垂足为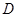 , 6分
, 6分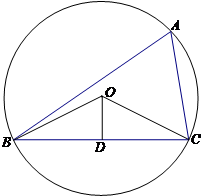
由(1)知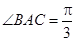 ,所以
,所以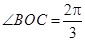 .
.
所以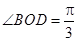 . 9分
. 9分
在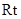 △
△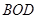 中,
中,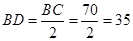 ,
,
所以
练习册系列答案
相关题目
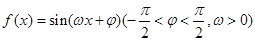 的最小正周期为
的最小正周期为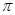 ,其图像经过点
,其图像经过点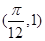
 的解析式;
的解析式;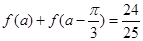 且
且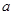 为锐角,求
为锐角,求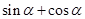 的值.
的值.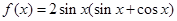 .
.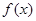 的最小正周期;
的最小正周期;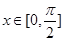 时,求
时,求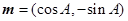 ,
,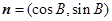 ,
,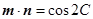 ,其中
,其中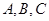 为
为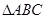 的内角.
的内角.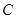 的大小;
的大小;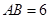 ,且
,且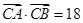 ,求
,求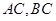 的长.
的长.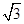 sinωxcosωx(ω>0)的最小正周期为π,
sinωxcosωx(ω>0)的最小正周期为π,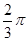 ]上的值域.
]上的值域.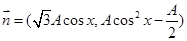 ,
, ,
,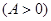 ,函数
,函数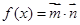 的最大值为
的最大值为 .
. ;
;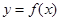 的图像向左平移
的图像向左平移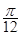 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的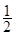 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数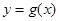 的图像,求
的图像,求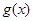 在
在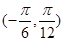 上的值域.
上的值域.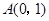 ,
,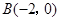 ,
,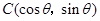 (
(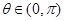 ),
),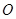 为坐标原点,向量
为坐标原点,向量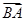 与向量
与向量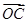 共线.
共线.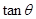 的值;
的值;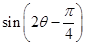 的值.
的值.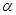 为第三象限角,
为第三象限角,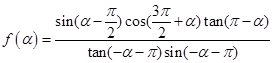 .
.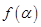 (2)若
(2)若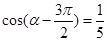 ,求
,求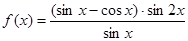
 的定义域及最小正周期;
的定义域及最小正周期;