题目内容
【题目】祖暅原理：两个等高的几何体，若在所有等高处的水平截面的面积相等，则这两个几何体的体积相等.利用祖暅原理可以求旋转体的体积.比如：设半圆方程为
，半圆与
轴正半轴交于点
，作直线
，
交于点
，连接
（
为原点），利用祖暅原理可得：半圆绕
轴旋转所得半球的体积与
绕轴旋转一周形成的几何体的体积相等.类比这个方法，可得半椭圆
绕轴旋转一周形成的几何体的体积是_________.
【答案】
【解析】
根据题意，作出立体图像，得到半椭圆
绕
轴旋转一周形成的几何体，然后直接求体积即可
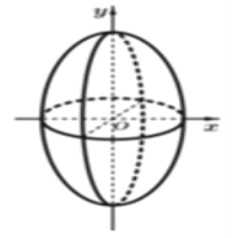
如图，这是椭圆绕轴旋转一周形成的几何体，所以
半椭圆绕轴旋转一周形成的几何体为：椭圆的长半轴为
，短半轴为
，现构造两个底面半径为，高为的圆柱，然后在圆柱内挖去一个以圆柱下底面圆心为顶点，圆柱上底面为底面的圆锥，根据祖暅原理，得出该几何体的体积是
；
答案：
练习册系列答案
相关题目
