题目内容
设命题p:函数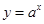 在R上单调递增,命题q:不等式
在R上单调递增,命题q:不等式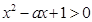
对于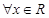 恒成立,若“
恒成立,若“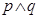 ”为假,“
”为假,“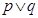 ”为真,求实数
”为真,求实数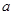 的取值范围
的取值范围
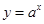 在R上单调递增,命题q:不等式
在R上单调递增,命题q:不等式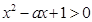
对于
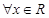 恒成立,若“
恒成立,若“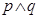 ”为假,“
”为假,“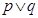 ”为真,求实数
”为真,求实数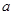 的取值范围
的取值范围解:∵命题p:函数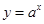 在R上单调递增,∴
在R上单调递增,∴ a>1
a>1
又命题q:不等式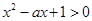 对于
对于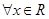 恒成立
恒成立
△=(-a)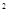 -4<0
-4<0
∴-2<a<2
∵“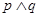 ”为假,“
”为假,“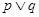 ”为真, ∴p,q必一真一假;
”为真, ∴p,q必一真一假;
(1)当p真,q假时,有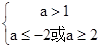
∴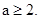
(2) 当p假,q真时,有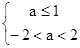
∴-2<a≤1.
综上, 实数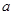 的取值范围为
的取值范围为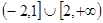 -------12分
-------12分
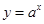 在R上单调递增,∴
在R上单调递增,∴ a>1
a>1又命题q:不等式
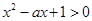 对于
对于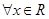 恒成立
恒成立△=(-a)
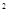 -4<0
-4<0 ∴-2<a<2
∵“
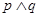 ”为假,“
”为假,“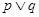 ”为真, ∴p,q必一真一假;
”为真, ∴p,q必一真一假;(1)当p真,q假时,有
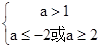
∴
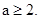
(2) 当p假,q真时,有
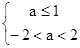
∴-2<a≤1.
综上, 实数
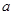 的取值范围为
的取值范围为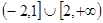 -------12分
-------12分本试题主要是考查了命题的真值和复合命题真值的判定的综合运用。
由于命题p:函数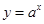 在R上单调递增,∴
在R上单调递增,∴ a>1
a>1
又命题q:不等式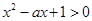 对于
对于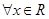 恒成立
恒成立
△=(-a)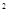 -4<0
-4<0
∴-2<a<2
那么利用已知条件p,q必一真一假;,分情况讨论得到结论。
由于命题p:函数
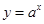 在R上单调递增,∴
在R上单调递增,∴ a>1
a>1又命题q:不等式
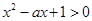 对于
对于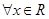 恒成立
恒成立△=(-a)
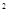 -4<0
-4<0 ∴-2<a<2
那么利用已知条件p,q必一真一假;,分情况讨论得到结论。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
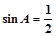 则
则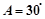
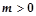 则
则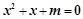 有实根
有实根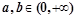 当
当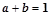 时
时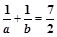
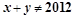 是
是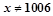 或
或 的充分不必要条件
的充分不必要条件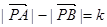 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;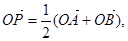 则动点P的轨迹为
则动点P的轨迹为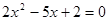 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率; 有相同的焦点.
有相同的焦点.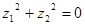 ,则复数
,则复数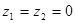
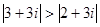
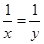 ,则
,则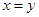
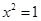 ,则
,则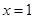
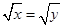
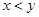 ,则
,则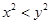
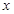 ,使
,使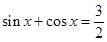 ;②若
;②若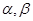 是第一象限角,且
是第一象限角,且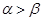 ,则
,则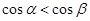 ;
;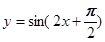 是偶函数; ④函数
是偶函数; ④函数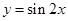 的图象向左平移
的图象向左平移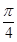 个单位,得到函
个单位,得到函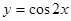 的图象.
的图象. 中至少有一个大于0
中至少有一个大于0 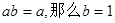
 一定也是0
一定也是0
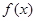 是定义在正整数集上的函数且满足当
是定义在正整数集上的函数且满足当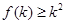 成立时,总可以推出
成立时,总可以推出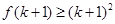 成立,则下列命题总成立的是( )
成立,则下列命题总成立的是( )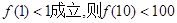 成立
成立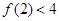 成立,则
成立,则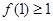 成立
成立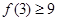 成立,则当
成立,则当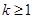 时,均有
时,均有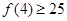 成立,则当
成立,则当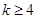 时,均有
时,均有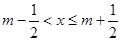 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即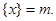 在此基础上给出下列关于函数
在此基础上给出下列关于函数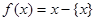 的四个命题:
的四个命题: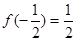 ;②
;②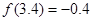 ;③
;③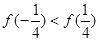 ;④
;④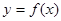 的定义域是R,
的定义域是R,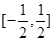 . 则其中真命题的序号是 ( )
. 则其中真命题的序号是 ( )