题目内容
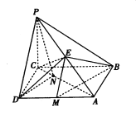
【题目】如图，在四棱锥
中，
底面
，底面是矩形，
，
是
的中点.
（1）求证：
平面
；
（2）已知点
是
的中点，点
是
上一点，且平面
平面
.若
，求点到平面的距离.
【答案】（1）证明见解析；（2）
.
【解析】
试题分析：（1）由题意可知，因为
，所以需要用到等腰三角形的三线合一的性质可得出需要取
的中点，然后证明
平面
，从而得到证明；（2）利用等体积转换的方法即可求出点
到平面的距离.
试题解析：（1）证明：取的中点为
，连接
和
，
∵
是
的中点，∴
，
∴平面与平面
为同一平面，
∵
底面
，底面是矩形，
∴
，即
平面
，∴
.
∵
，∴平面.
（2）过
作
交
于
，连接
，
∵
是
的中点，∴
，
∵
，
平面
平面
，
∴当是
与
的交点时，平面
平面，
在矩形中，求得
，
∵
，∴
，
到平面的距离为
，设点到平面的距离为
，
由
得
，解得
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】为了参加市高中篮球比赛，某中学决定从四个篮球较强的班级的篮球队员中选出
人组成男子篮球队，代表该地区参赛，四个篮球较强的班级篮球队员人数如下表：
班级 | 高三（7）班 | 高三（17）班 | 高二（31）班 | 高二（32）班 |
人数 | 12 | 6 | 9 | 9 |
（1）现采取分层抽样的方法从这四个班中抽取运动员，求应分别从这四个班抽出的队员人数；
（2）该中学篮球队奋力拼搏，获得冠军.若要从高三年级抽出的队员中选出两位队员作为冠军的代表发言，求选出的两名队员来自同一班的概率.
