题目内容

2．下列求导运算正确的是（　　）
A．（x+$\frac{1}{x}$）′=1+$\frac{1}{{x}^{2}}$B．$（\frac{{e}^{x}}{x}）′$=$\frac{{e}^{x}+x{e}^{x}}{{x}^{2}}$
C．（x2sinx）′=2xcosxD．（log2x）′=$\frac{1}{xln2}$

分析 根据导数的运算公式计算即可．

解答 解：（x+$\frac{1}{x}$）′=1-$\frac{1}{{x}^{2}}$，
$（\frac{{e}^{x}}{x}）′$=$\frac{{xe}^{x}-{e}^{x}}{{x}^{2}}$，
（x2sinx）′=2xsin+x2cosx，
（log2x）′=$\frac{1}{xln2}$，
故选：D．

点评 本题考查了导数的运算法则，属于基础题．

练习册系列答案
相关题目
12．已知函数f（x）=ex，g（x）=m-x，m∈R．
（1）记h（x）=f（x）•g（x），求h（x）的极值；
（2）当m=0时，试比较ef（x-2）与-g（x）的大小．
13．已知一扇形的圆心角为α（α＞0），所在圆的半径为R．
（1）若α=60°，R=10cm，求扇形的弧长及该弧所在的弓形的面积；
（2）一扇形的周长为20cm，当扇形的圆心角α等于多少弧度时，这个扇形的面积最大？
10．已知函数f（x）=2sin（ωx+φ）（ω＞0，0＜|φ|＜$\frac{π}{2}$）的图象上，直线x=x1，x=x2是y=f（x）图象的任意两条对称轴，且|x1-x2|的最小值为$\frac{π}{2}$．
（I）求函数f（x）的单调递增区间；
（II）设A={x|$\frac{π}{4}$≤x≤$\frac{π}{2}$}，B={x||f（x）-m|＜1}，若A⊆B，求实数m的取值范围；
（III）若已知cosα+$\frac{1}{2}$f（$\frac{α}{2}$+$\frac{π}{6}$）=$\frac{2}{3}$，求$\frac{\sqrt{2}sin（2α-\frac{π}{4}）+1}{1+tanα}$的值．
17．甲、乙两同学5次综合评测的成绩如茎叶图所示．老师发现乙同学成绩的一个数字无法看清．但老师知道乙的平均成绩超过甲的平均成绩，则看不清楚的数字为9．
7．某保险公司推出了一种保期为一年的险种：若投保人在投保一年内意外死亡，则公司赔偿20万元，若投保人因大病住院治疗（医疗费超过10万元者），则公司赔付10万元，否则公司无需赔付任何费用，通过大数据显示投保人在一年意外死亡的概率为0.0001，大病住院治疗的概率为0.002．
（Ⅰ）某个家庭的夫妻两人都买了此险种，求他们在投保期末获得赔付金额的分布列和期望；
（Ⅱ）若有一万个客户投保，每份保单的投保费用是300元/年，问保险公司在此险种中一年的盈利是多少．
14．如图直观图由直三棱柱与圆锥组成的几何体，其三视图的正视图为正方形，则俯视图中的椭圆的离心率为（　　）
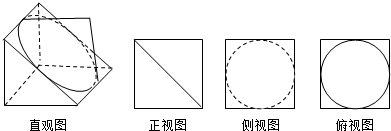
A．$\frac{\sqrt{2}}{3}$B．$\frac{1}{2}$C．$\frac{\sqrt{2}}{4}$D．$\frac{\sqrt{2}}{2}$
5．已知函数f（x）=-x2+ax，g（x）=2lnx-b，且两函数在x=2处有相同的切线．
（1）求两函数的解析式；
（2）是否存在实数m，使得函数y=f（x）+m的图象与y=g（x）的图象有且仅有三个不同的交点？若存在，求实数m的取值范围；若不存在，请说明理由．
6．求适合下列等式的x与y（x，y∈R）的值：（$\frac{1}{2}$x+y）+（5x+$\frac{2}{3}$y）i=-4+16i．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网