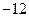题目内容
求 在点
在点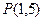 和
和 处的切线方程。
处的切线方程。
 在点
在点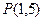 和
和 处的切线方程。
处的切线方程。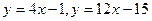
点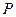 在函数的曲线上,因此过点
在函数的曲线上,因此过点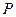 的切线的斜率就是
的切线的斜率就是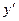 在
在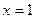 处的函数值;
处的函数值;
点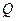 不在函数曲线上,因此不能够直接用导数求值,要通过设切点的方法求切线.切忌直接将
不在函数曲线上,因此不能够直接用导数求值,要通过设切点的方法求切线.切忌直接将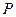 ,
,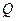 看作曲线上的点用导数求解。
看作曲线上的点用导数求解。
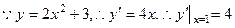
即过点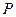 的切线的斜率为4,故切线为:
的切线的斜率为4,故切线为: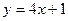 .
.
设过点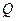 的切线的切点为
的切线的切点为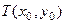 ,则切线的斜率为
,则切线的斜率为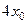 ,又
,又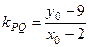 ,
,
故 ,
,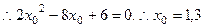 。
。
即切线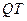 的斜率为4或12,从而过点
的斜率为4或12,从而过点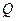 的切线为:
的切线为: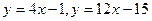
 在函数的曲线上,因此过点
在函数的曲线上,因此过点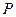 的切线的斜率就是
的切线的斜率就是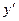 在
在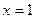 处的函数值;
处的函数值;点
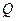 不在函数曲线上,因此不能够直接用导数求值,要通过设切点的方法求切线.切忌直接将
不在函数曲线上,因此不能够直接用导数求值,要通过设切点的方法求切线.切忌直接将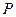 ,
,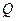 看作曲线上的点用导数求解。
看作曲线上的点用导数求解。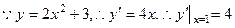
即过点
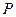 的切线的斜率为4,故切线为:
的切线的斜率为4,故切线为: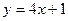 .
.设过点
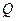 的切线的切点为
的切线的切点为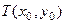 ,则切线的斜率为
,则切线的斜率为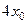 ,又
,又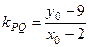 ,
,故
 ,
,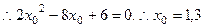 。
。即切线
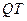 的斜率为4或12,从而过点
的斜率为4或12,从而过点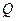 的切线为:
的切线为: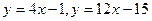

练习册系列答案
相关题目
 =x.
=x. 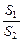 的解析式并求f(x)的定义域.
的解析式并求f(x)的定义域. 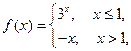 若
若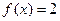 ,则
,则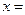 .
.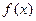 ,
,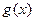 是定义在R上的函数,
是定义在R上的函数,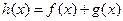 ,则“
,则“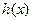 为偶函数”的
为偶函数”的 的切线垂直于直线
的切线垂直于直线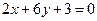 ,试求这条切线的方程。
,试求这条切线的方程。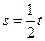 ,该质点在
,该质点在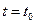 时的瞬时速度 。
时的瞬时速度 。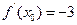 ,则
,则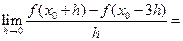 ( )
( )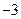 B
B 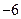
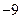 D
D