题目内容
正四棱锥P-ABCD的侧棱长和底面边长都等于a，有两个正四面体的棱长也都等于a．当这两个正四面体各有一个面与正四棱锥的侧面PAD，侧面PBC完全重合时，得到一个新的多面体，该多面体是（ ）
分析：由正四棱锥的相邻二个侧面所成的二面角为arccos（-
），可知得到的新多面体为五面体．
| 1 |
| 3 |
解答：解：正四面体每相邻二个面所成的二面角为arccos
，
题目所说的正四棱锥的相邻二个侧面所成的二面角为arccos（-
），
所以得到的新多面体为五面体．
故选A．
| 1 |
| 3 |
题目所说的正四棱锥的相邻二个侧面所成的二面角为arccos（-
| 1 |
| 3 |
所以得到的新多面体为五面体．
故选A．
点评：本题考查棱锥的结构特征，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
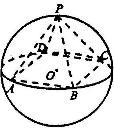如图，正四棱锥P-ABCD底面的四个顶点A、B、C、D在球O的同一个大圆上，点P在球面上，如果VP-ABCD=| 16 |
| 3 |
| A、4π | B、8π |
| C、12π | D、16π |
（2009•温州一模）如图是正四棱锥P-ABCD的三视图，其中正视图是边长为1的正三角形，则这个四棱锥的表面积是（ ）