Question

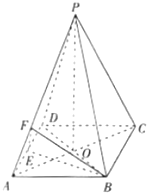如图，已知四棱锥P-ABCD的底面积是菱形，AC交BD于O，PO⊥平面ABC，E为AD中点，F在PA上，AP=λAF，PC∥平面BEF．
（1）求λ的值；
（2）若AB=2，∠ADB=∠BPC=60°，求三棱锥A-EFB的体积．

Answer 1

分析：（1）由线面平行得线线平行，利用比例关系得λ的值；
（2）利用等积法把三棱锥A-EFB的体积转化为求三棱锥F-ABE的体积．

解答：解：（1）设AO交BE于G，连接FG．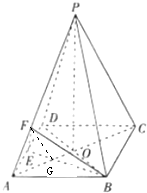
因为O，E分别是BD、AD的中点，所以

AG

AO

=

2

3

，

AG

AC

=

1

3

因为PC∥平面BEF，所以GF∥PC
所以

AF

AP

=

AG

AC

=

1

3

．即λ=3
（2）因为∠BPD=60°，PO⊥平面ABC，所以PO=

3

故点F到平面ABC的距离为

1

3

PO=

3

3

所以VA-EFB=VF-ABE=

1

3

×

3

2

×

3

3

=

1

6

故三棱锥A-EFB的体积为

1

6

点评：本题主要考查了线面平行的性质，几何体体积的求法．