题目内容
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)若存在![]() ,使得
,使得![]() (
(![]() 是自然对数的底数),求实数
是自然对数的底数),求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 单调递增;在
单调递增;在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】试题分析:(1)依据题设条件先求导再运用导数与函数的单调性之间的关系分析探求;(2)先将不等式进行等价转化,再构造函数运用导数的知识分析探求:
试题解析:
解:(1)![]()
![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时
时![]() ;当
;当![]() 时
时![]() .
.
故函数![]() 在
在![]() 单调递增;在
单调递增;在![]() 上单调递减.
上单调递减.
(2)因为存在![]() ,使得
,使得![]() 成立,
成立,
而当![]() 时,
时,![]() ,
,
所以只要![]() 即可.
即可.
又因为![]() ,
,![]() ,
,![]() 的变化情况如下表所示:
的变化情况如下表所示:
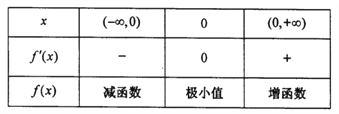
所以![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,所以当
上是增函数,所以当![]() 时,
时,![]() 的最小值
的最小值![]() ,
,![]() 的最大值
的最大值![]() 为
为![]() 和
和![]() 中的最大值.
中的最大值.
因为![]()
![]() ,
,
令![]() ,因为
,因为![]() ,
,
所以![]() 在
在![]() 上是增函数.
上是增函数.
而![]() ,故当
,故当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() .
.
所以,当![]() 时,
时,![]() ,即
,即![]() ,
,
函数![]() 在
在![]() 上是增函数,解得
上是增函数,解得![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,
,
函数![]() 在
在![]() 上是减函数,解得
上是减函数,解得![]() .
.
综上可知,所求![]() 的取值范围为
的取值范围为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用 | 过度使用 | 合计 | |
未患颈椎病 | 15 | 5 | 20 |
患颈椎病 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据与公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()